Abstract¶
Cette section présente les concepts fondamentaux du traitement des signaux, essentiels pour comprendre et analyser les systèmes de communication. Elle aborde les définitions, classifications et opérations de base des signaux. L’analyse de Fourier y est développée pour explorer la décomposition des signaux en composantes fréquentielles. Les principes de modulation d’amplitude et les systèmes linéaires invariants dans le temps (LTI) sont également discutés, avec un accent sur des notions clés telles que la largeur de bande, la densité spectrale de puissance, l’autocorrélation et les filtres. Enfin, la section introduit les signaux aléatoires, en se concentrant sur les distributions gaussiennes, les moyennes statistiques et le théorème de la limite centrale, établissant ainsi une base solide pour l’étude des signaux dans des environnements variés.
Signal¶
- Définition: Signal
- Un signal est une fonction qui transmet des informations sur un phénomène.
Les signaux constituent les entrées et les sorties des systèmes. Un signal peut être classé selon différents critères. Les critères que nous allons examiner sont énumérés ci-dessous.
Signaux à temps continu et à temps discret:
Un signal à temps continu est un signal pour lequel la variable indépendante prend des nombres réels.
Un signal à temps discret, noté , est un signal pour lequel la variable indépendante prend ses valeurs dans l’ensemble des entiers.
En échantillonnant un signal à temps continu à des instants séparés par , nous pouvons définir le signal à temps discret . Ici, est l’indice de temps, représentant le ième échantillon.
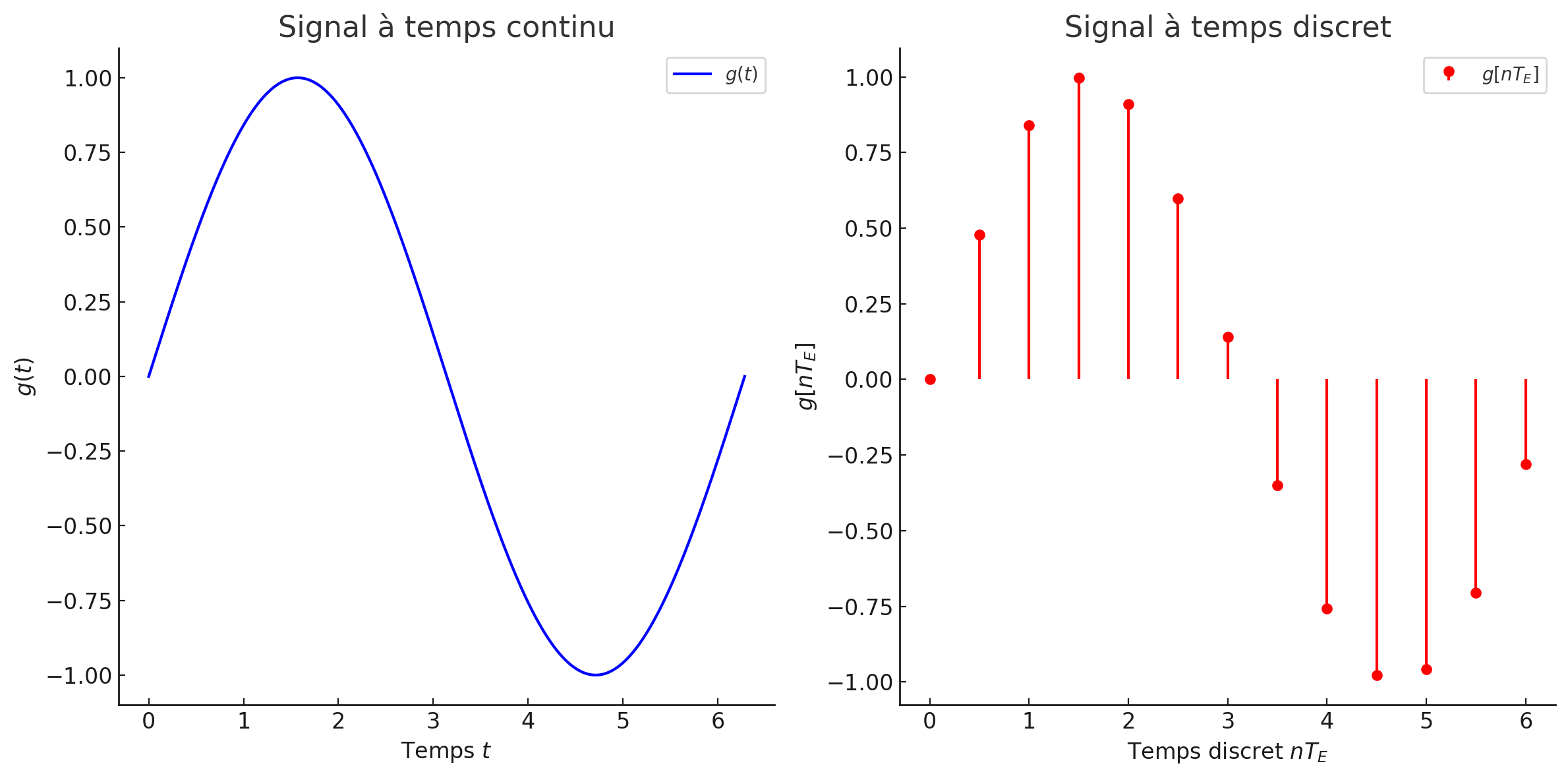
Figure 1:Signaux à temps continu et à temps discret (la période d’échantillonnage est de unités de temps).
Signaux analogiques et numériques
Un signal dont l’amplitude peut prendre n’importe quelle valeur dans une gamme continue est un signal analogique.
- Cela signifie que l’amplitude d’un signal analogique peut prendre un nombre (indénombrable) infini de valeurs.
Un signal numérique, par contre, est un signal dont l’amplitude ne peut prendre qu’un nombre fini de valeurs.
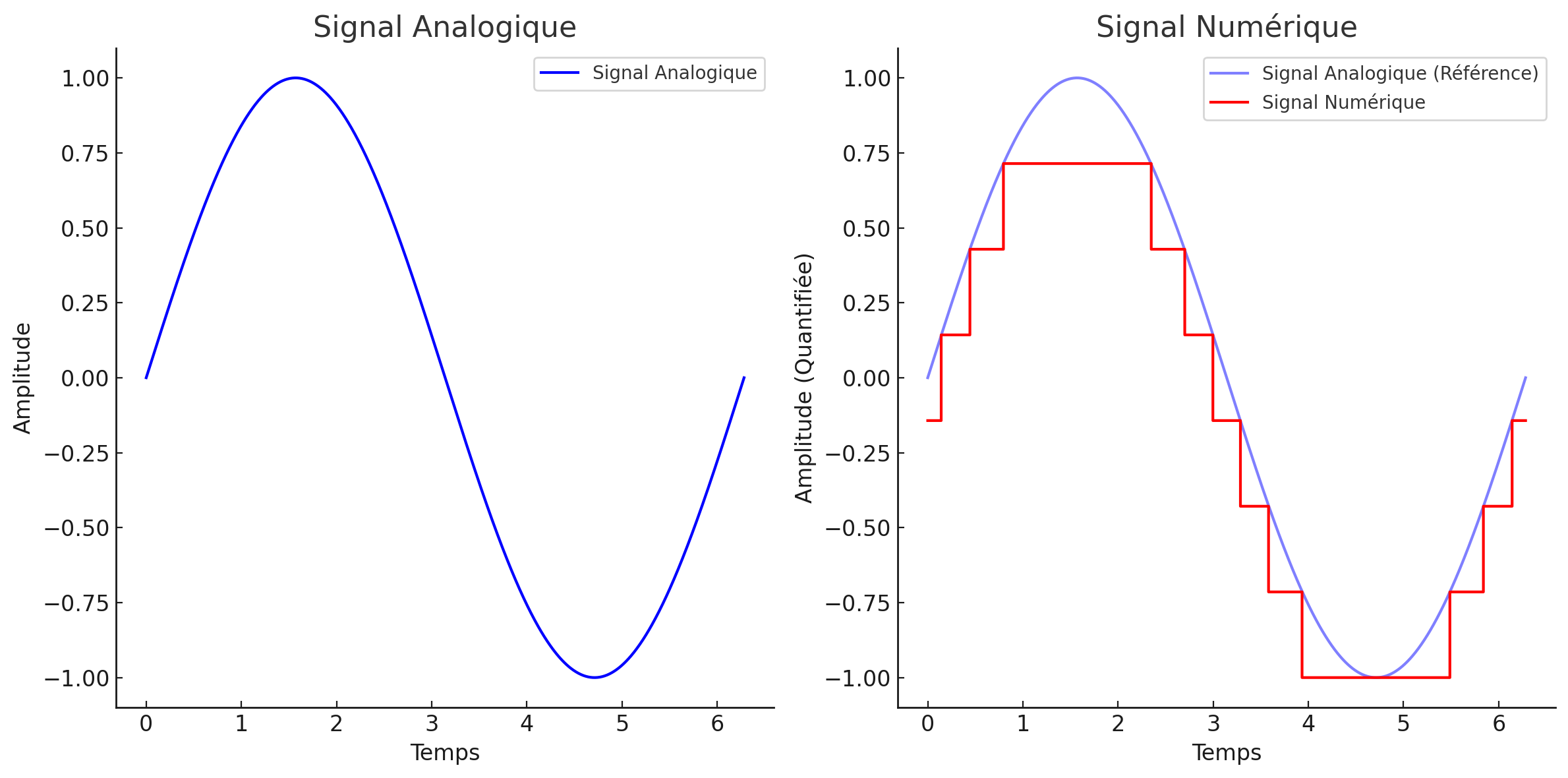
Figure 2:Signaux analogiques et numériques.
Signaux périodiques et non périodiques.
Un signal périodique se répète dans le temps ; il suffit donc de spécifier le signal dans un intervalle de base appelé période, , Pour un signal signal périodique :
Un signal non périodique ne se répète pas dans le temps.
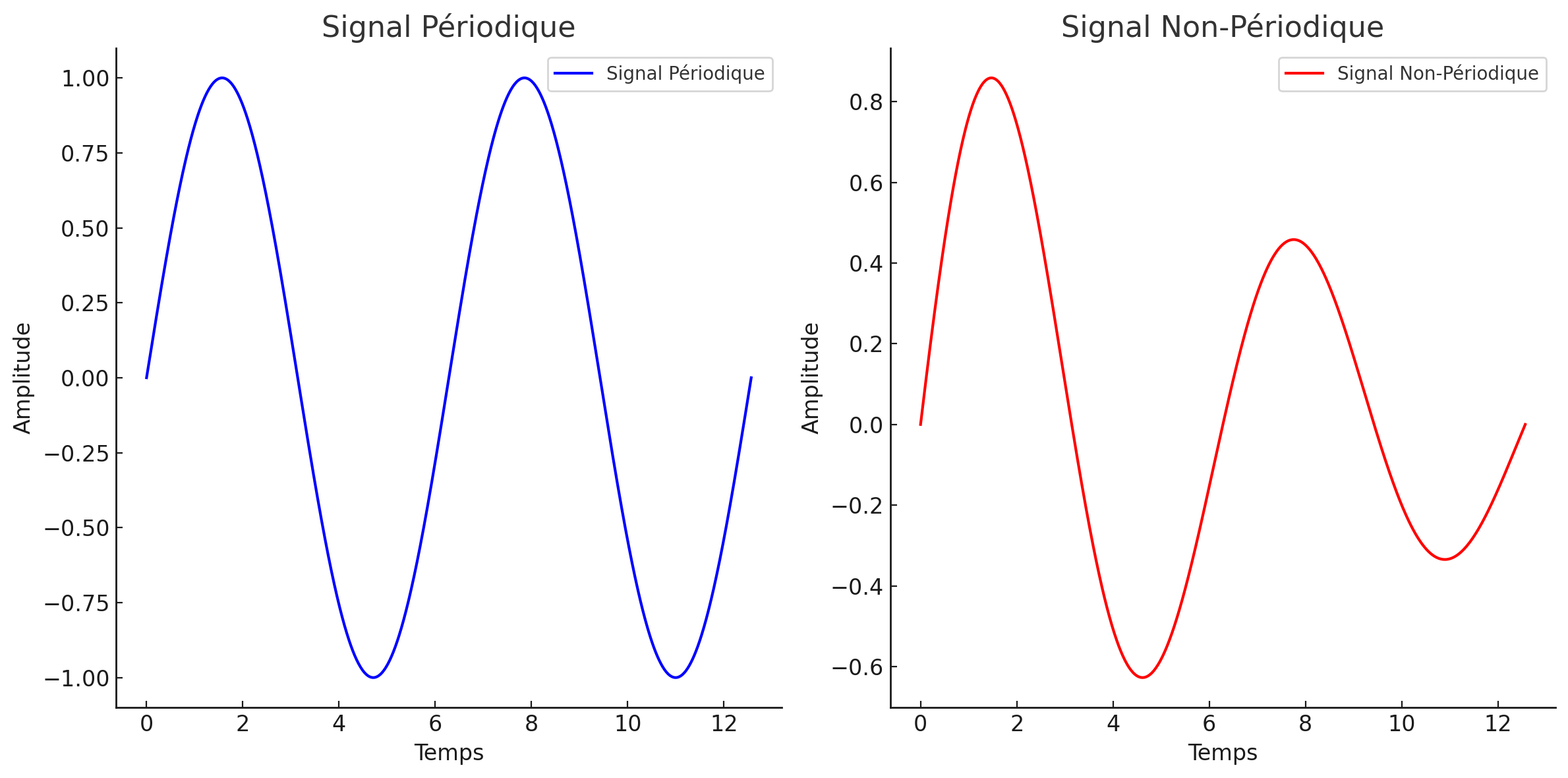
Figure 3:Signaux périodiques (où unités de temps) et non périodiques.
Signaux réels et complexes.
Un signal réel prend ses valeurs dans l’ensemble des nombres réels,
Un signal complexe prend ses valeurs dans l’ensemble des nombres complexes .
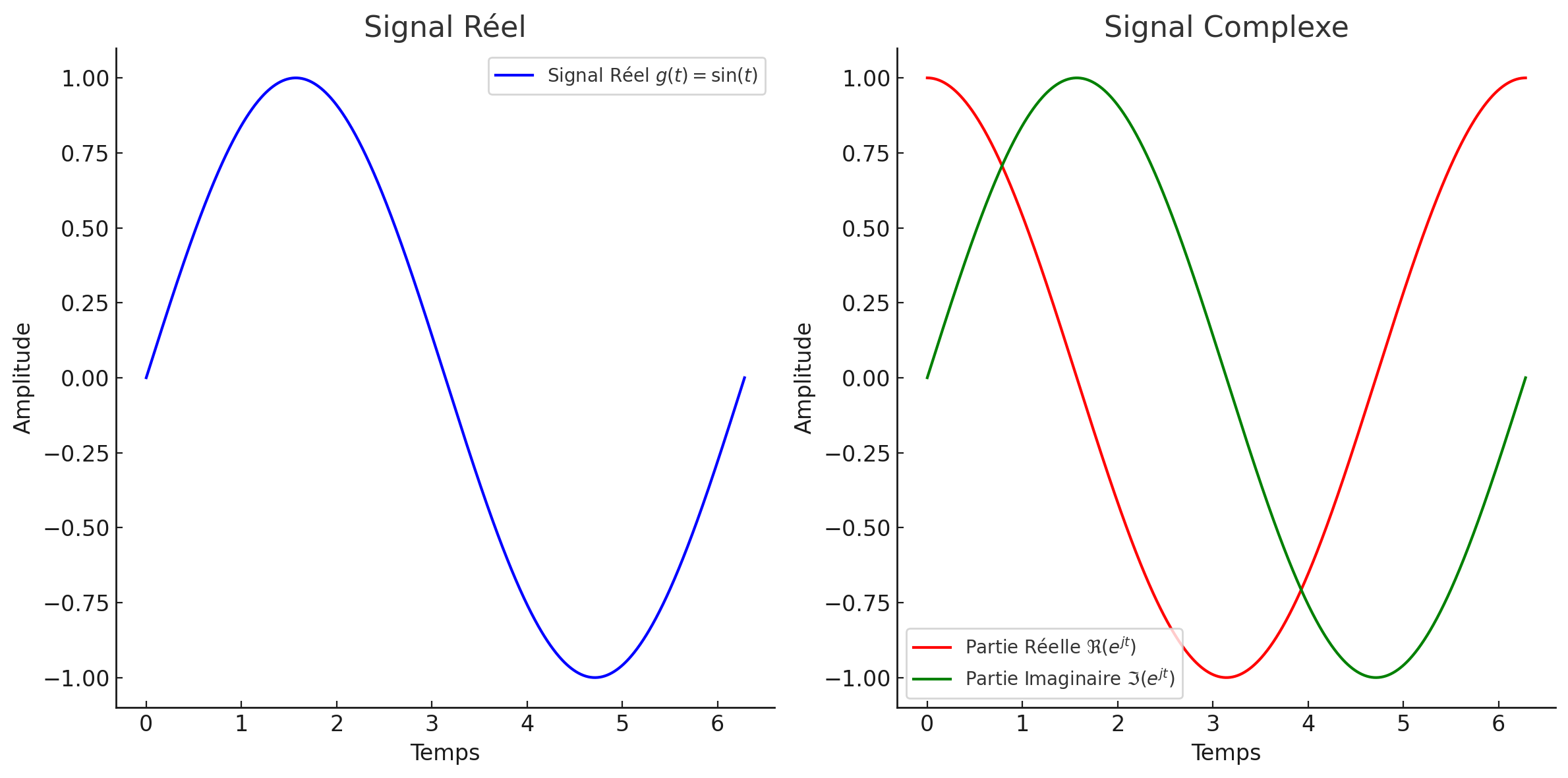
Figure 4:Signaux réels et complexes. Le signal réel est l’onde sinusoïdale . Le signal complexe est , dont les parties réelle et imaginaire sont tracées séparément.
Signaux déterministes et aléatoires.
Dans un signal déterministe, à tout instant , la valeur de est donnée comme une valeur réelle ou complexe.
Dans un signal aléatoire (ou stochastique), à un instant donné , est une variable aléatoire, c’est-à-dire qu’elle est définie par une fonction de densité de probabilité.
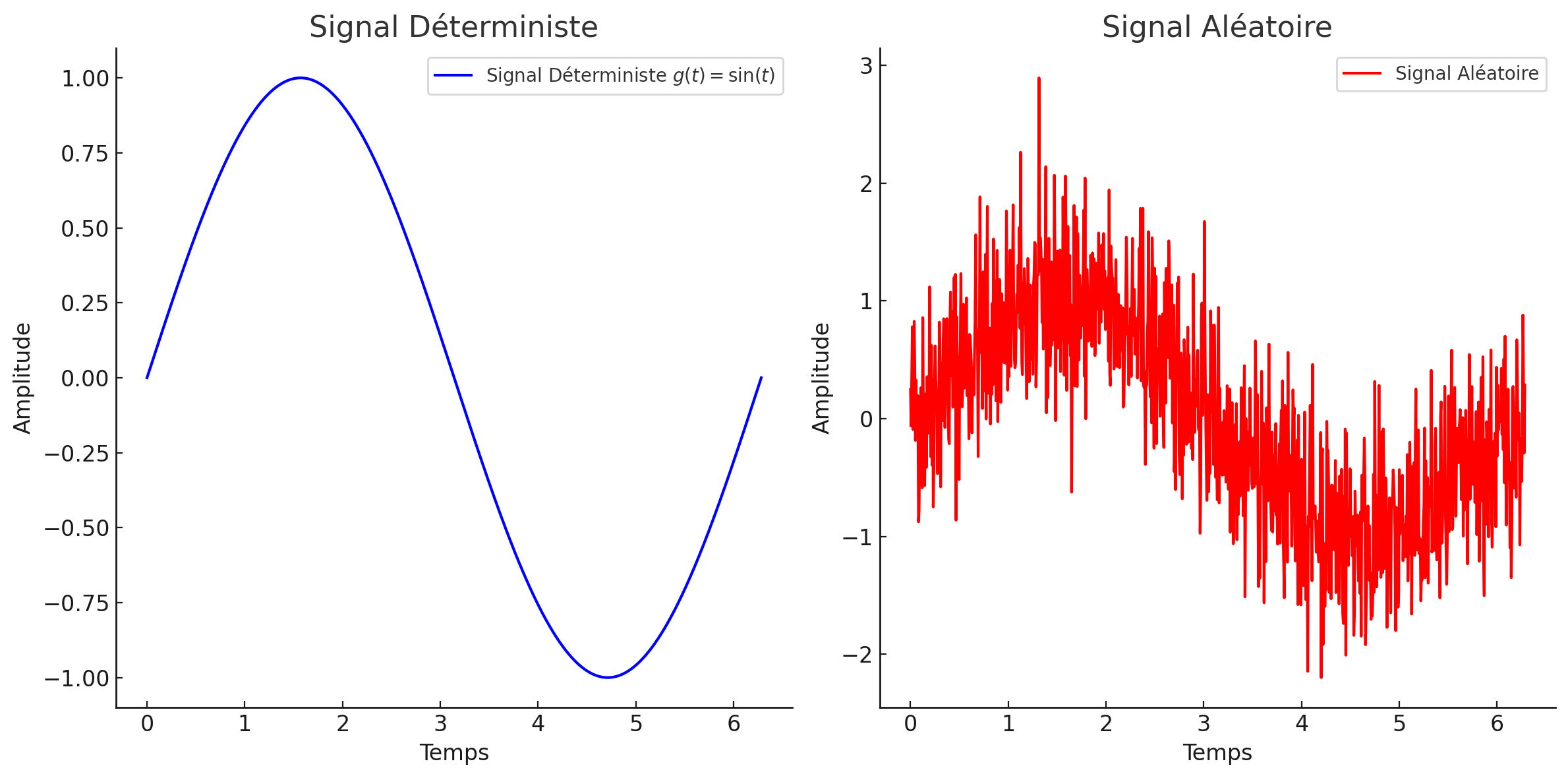
Figure 5:Signaux déterministes et aléatoires. Le signal déterministe est parfaitement prévisible à tout instant . Chaque valeur est fixée et définie. Le signal aléatoire est une superposition d’une onde sinusoïdale et d’un bruit gaussien aléatoire. La valeur de à un instant donné est imprévisible et suit une distribution aléatoire (donc les valeurs sont imprévisibles).
Notez que toutes ces représentations sont du domaine temporel. Pour pouvoir comprendre le comportement spectral, nous devons également analyser les signaux dans le domaine fréquentiel.
Représentation fréquentielle des signaux¶
Dans ce cours, nous utiliserons la transformée de Fourier pour représenter les signaux, même pour les signaux périodiques
- Définition: Transformée de Fourier
- La transformée de Fourier d’un signal est représentée par , et
Propriétés :
homogénéité de la transformée de Fourier stipule que la transformée de Fourier d’un signal multiplié par un constant scalaire est égale à la transformée de Fourier du signal, également multiplié par cette constante. Si est un signal avec et est un constant scalaire, :
Cela montre que l’échelle d’amplitude dans le domaine temporel est directement reflétée dans le domaine fréquentiel.
superposition de la transformée de Fourier découle directement de la linéarité. Si un signal est composé de plusieurs composantes, telles que , avec , sa transformée de Fourier est donnée par :
L’homogénéité et la superposition garantissent la linéarité de la transformée de Fourier, permettant ainsi que la transformée d’une combinaison linéaire de signaux, soit égale à la même combinaison linéaire, de leurs transformées respectives. La linéarité est fondamentale en analyse de Fourier, car elles permettent de décomposer des signaux complexes en une somme de signaux plus simples.
Propriétés d’un signal¶
Valeur moyenne¶
Énergie¶
Puissance¶
Notez que .
Tension efficace¶
Largeur de bande¶
- Définition: Largeur de bande
- La largeur de bande correspond à l’étendue des fréquences disponibles pour la transmission d’un signal. La largeur de bande d’un signal est une mesure de l’étendue de fréquences contenues dans le signal. En termes simples, elle représente la différence entre les fréquences les plus élevées et les plus basses et significatives dans le spectre du signal.
Un signal peut être classé comme bande de base ou bande passante selon sa concentration dans le domaine fréquentiel.
- Définition: Signal bande de base (baseband)
- Un signal bande de base est caractérisé par un contenu fréquentiel concentré autour de 0 Hz.
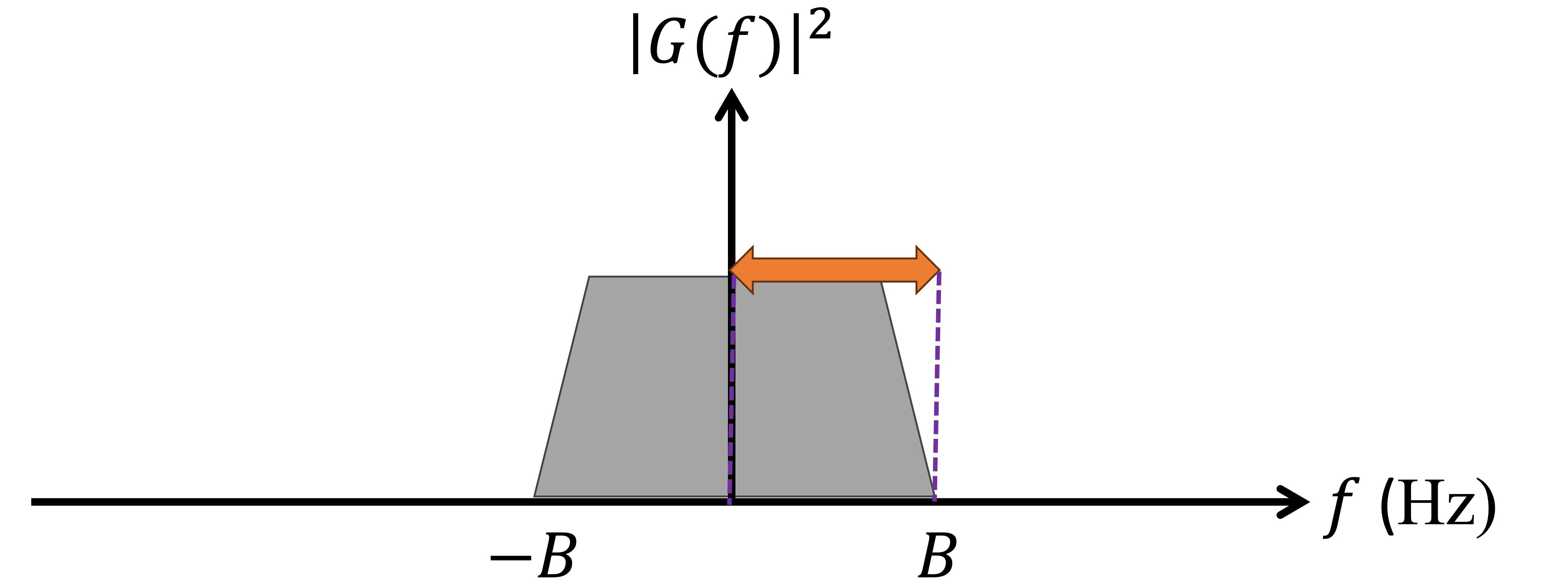
Figure 8:Réponse fréquentielle d’un signal en bande de base autour de , et la largeur de bande est de Hz.
- Définition: Signal bande passante (passband)
- Un signal bande passante est généralement obtenu après une modulation, c’est-à-dire après multiplication du signal bande de base par une onde porteuse, telle qu’une sinusoïde . Le contenu fréquentiel d’un signal bande passante est concentré autour de la fréquence porteuse, Hz.
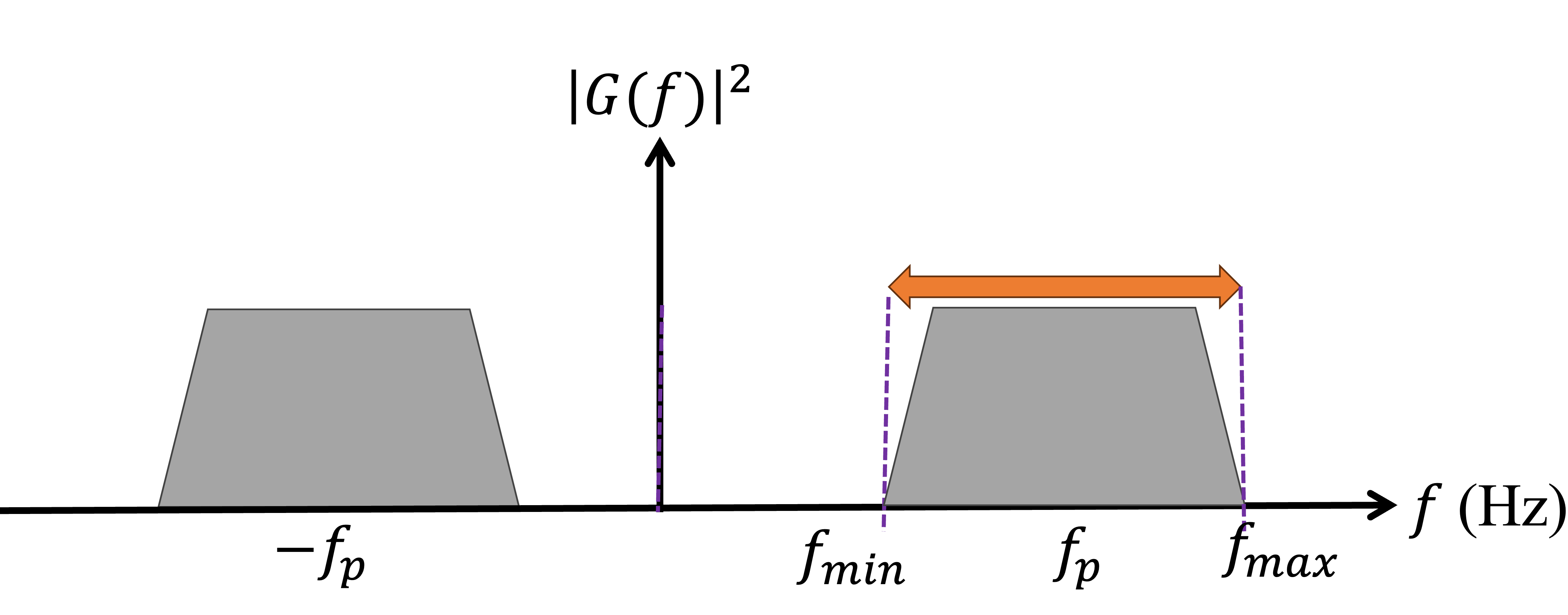
Figure 9:Réponse fréquentielle d’un signal en bande passante où la largeur de bande est de
Signaux utiles¶
Impulsion de Dirac (Dirac impulse)¶
- Définition: Impulsion de Dirac
- L’impulsion de Dirac est un outil mathématique idéal utilisé pour modéliser une impulsion infiniment brève et intense, qui ne peut pas être réalisée exactement dans la réalité physique.
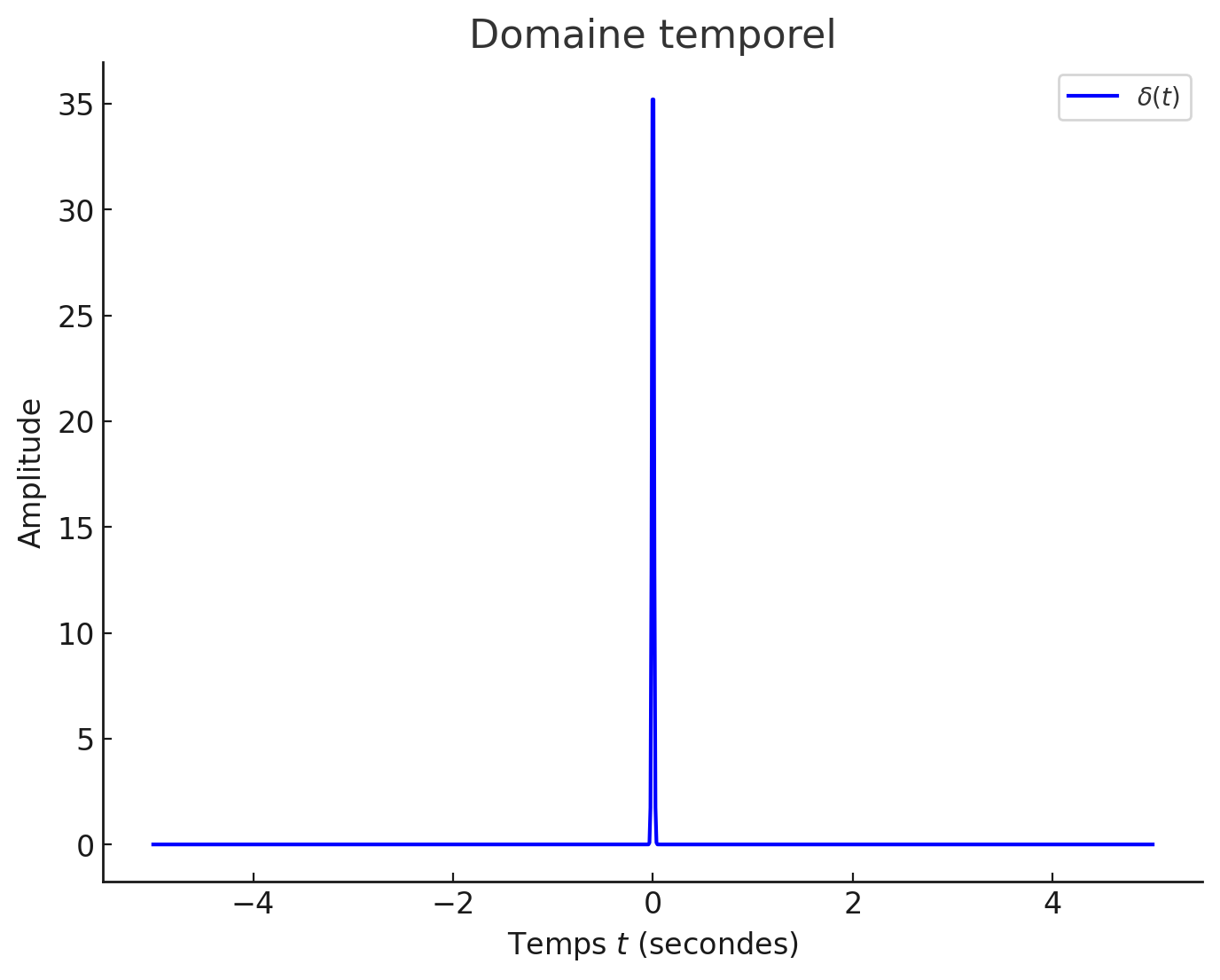
Figure 10:Impulsion de Dirac (en domaine temporel).
Propriétés:
Multiplication par l’impulsion de Dirac
Échantillonnage pour obtenir une seule valeur à
La valeur moyenne, l’énergie et la puissance de l’impulsion de Dirac sont indéfinies
La transformée de Fourier de est une fonction constante dans le domaine fréquentiel, donc ,
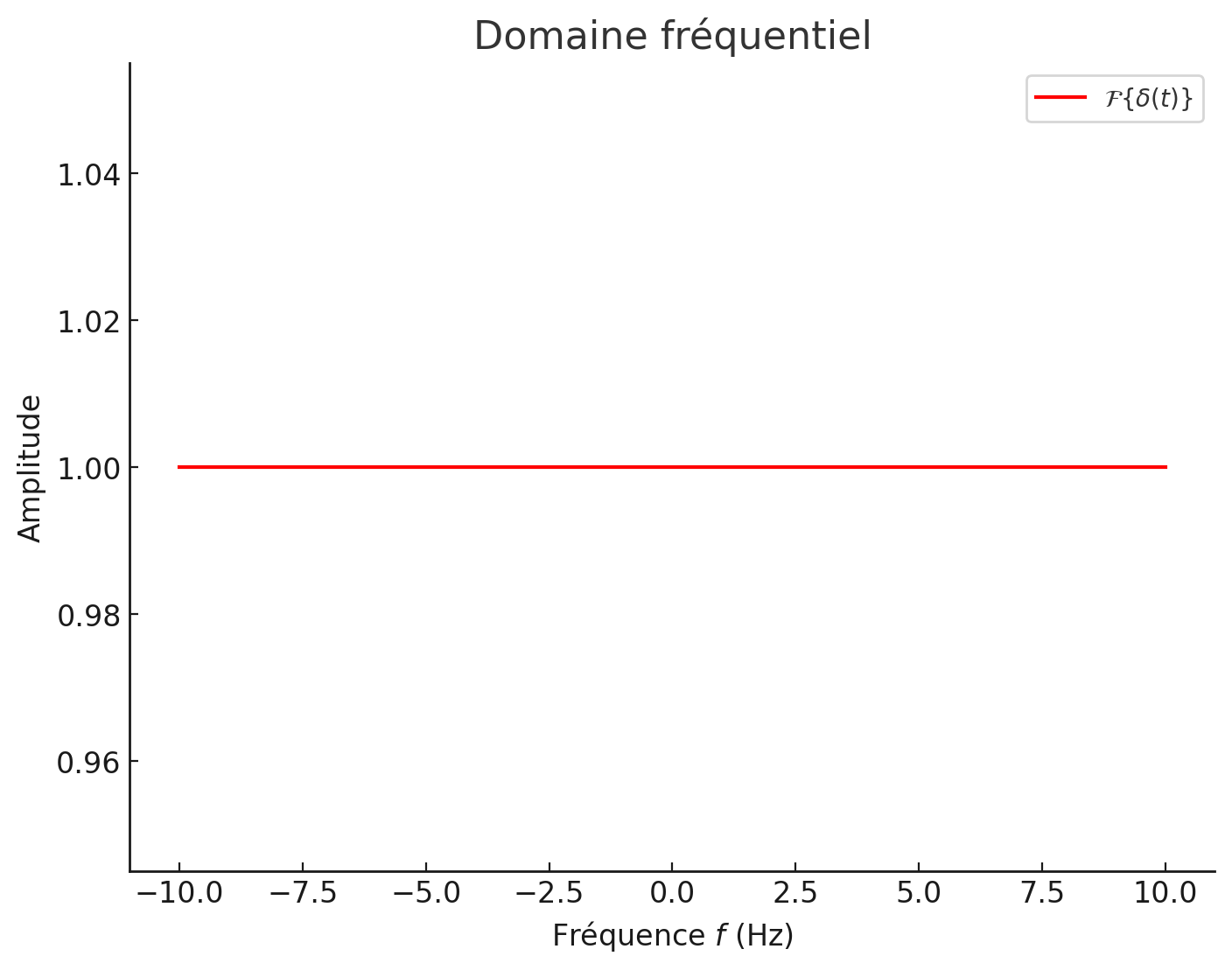
Figure 11:Impulsion de Dirac (en domaine fréquentiel).
Train d’impulsions de Dirac (Dirac impulse train)¶
- Définition: Train d’impulsions de Dirac
- La fonction train d’impulsions de Dirac, notée , est définie comme une somme infinie d’impulsions de Dirac espacées de secondes :
Propriétés:
La valeur moyenne :
L’énergie : infinie
La puissance :
La transformée de Fourier :
Fonction sinc (Sinc function)¶
- Définition: Fonction sinc
- La fonction est définie comme suit
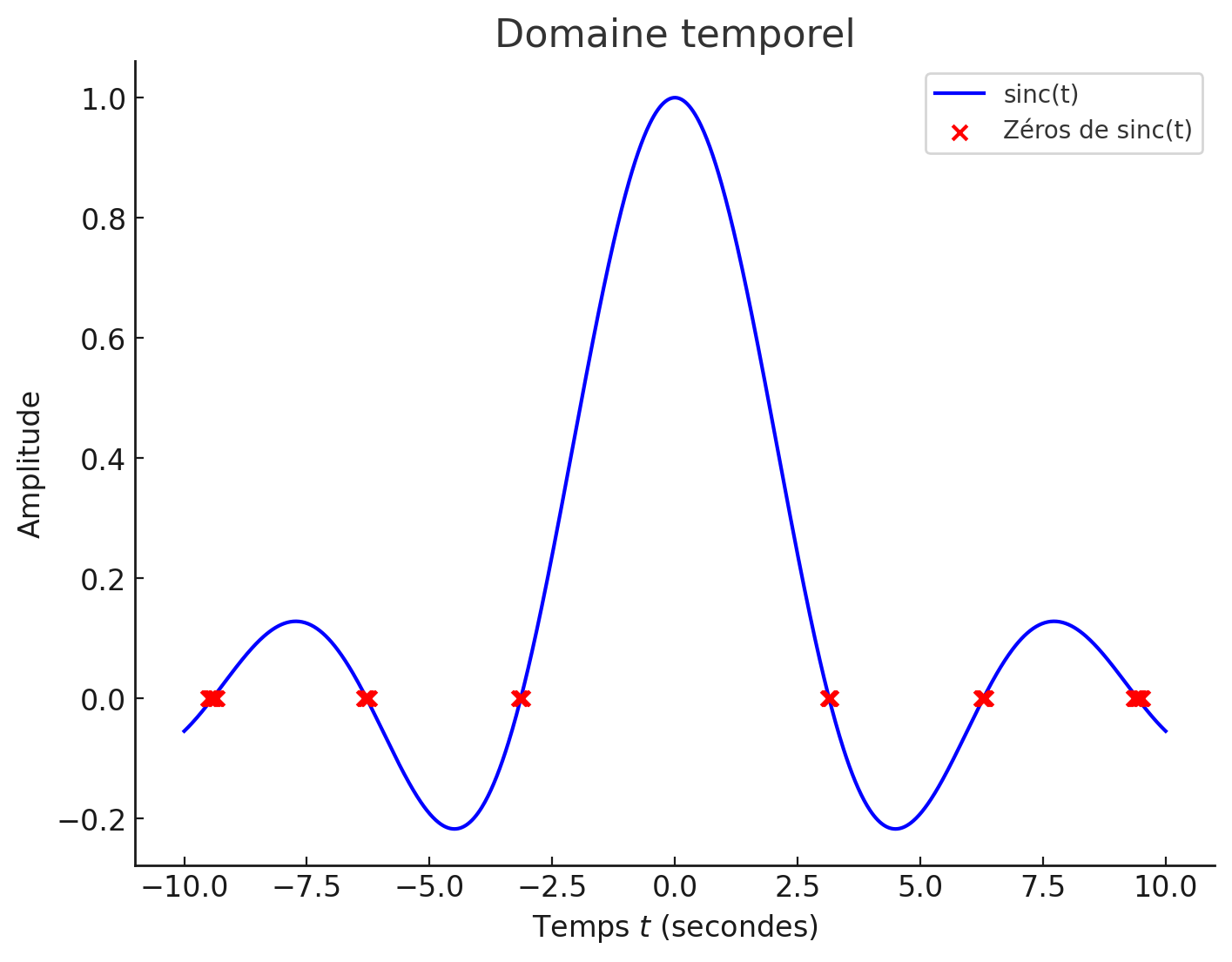
Figure 12:Fonction sinc (en domaine temporel).
Propriétés:
La valeur moyenne :
et converge vers zéro lorsque .
L’énergie :
qui augmente indéfiniment lorsque .
La puissance :
La transformée de Fourier :
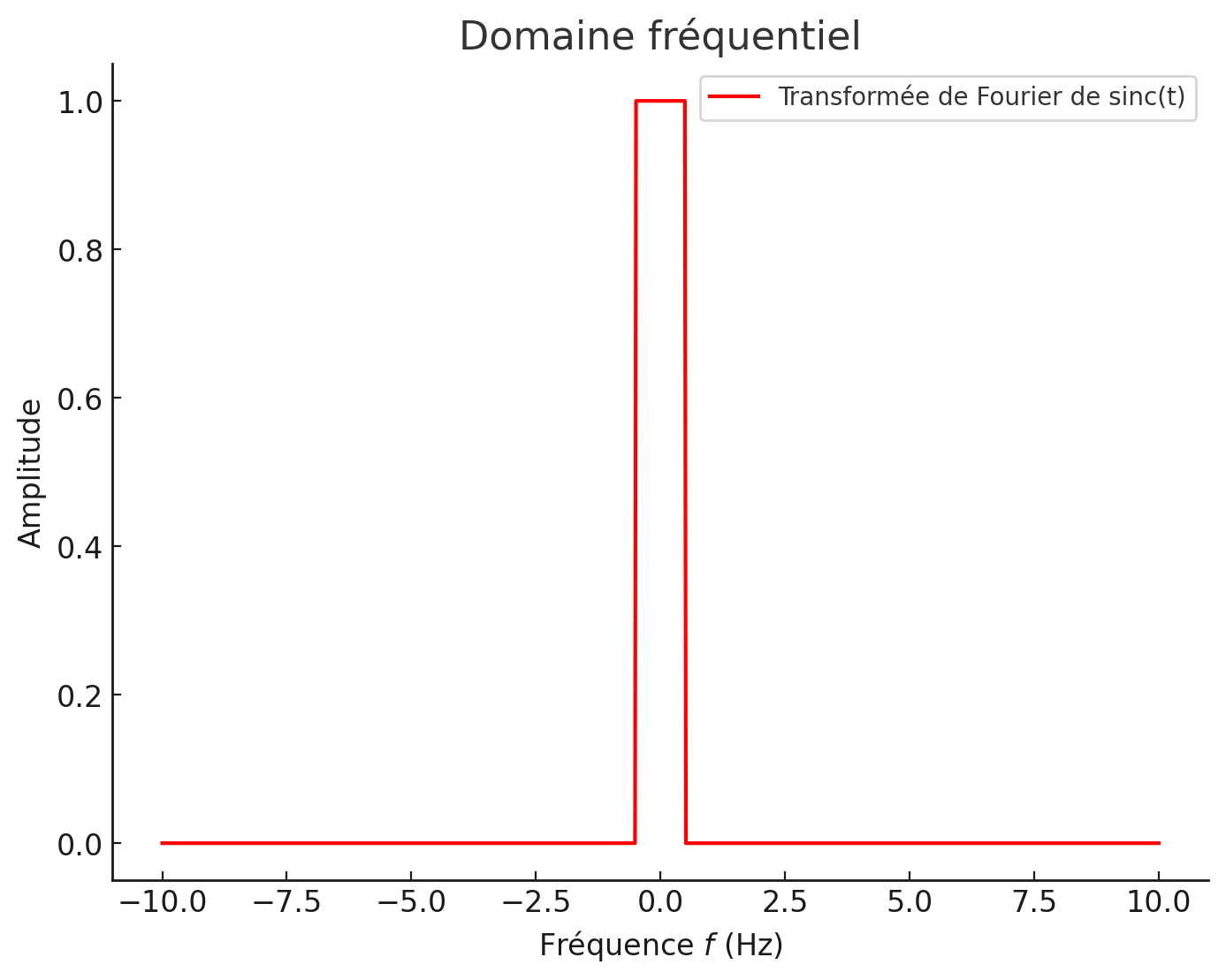
Figure 13:Fonction sinc (en domaine fréquentiel).
L’onde rectangulaire (Rectangular pulse)¶
- Définition: L’onde rectangulaire
- La fonction rectangulaire , définie sur l’intervalle , avec une valeur constante , est donnée par :
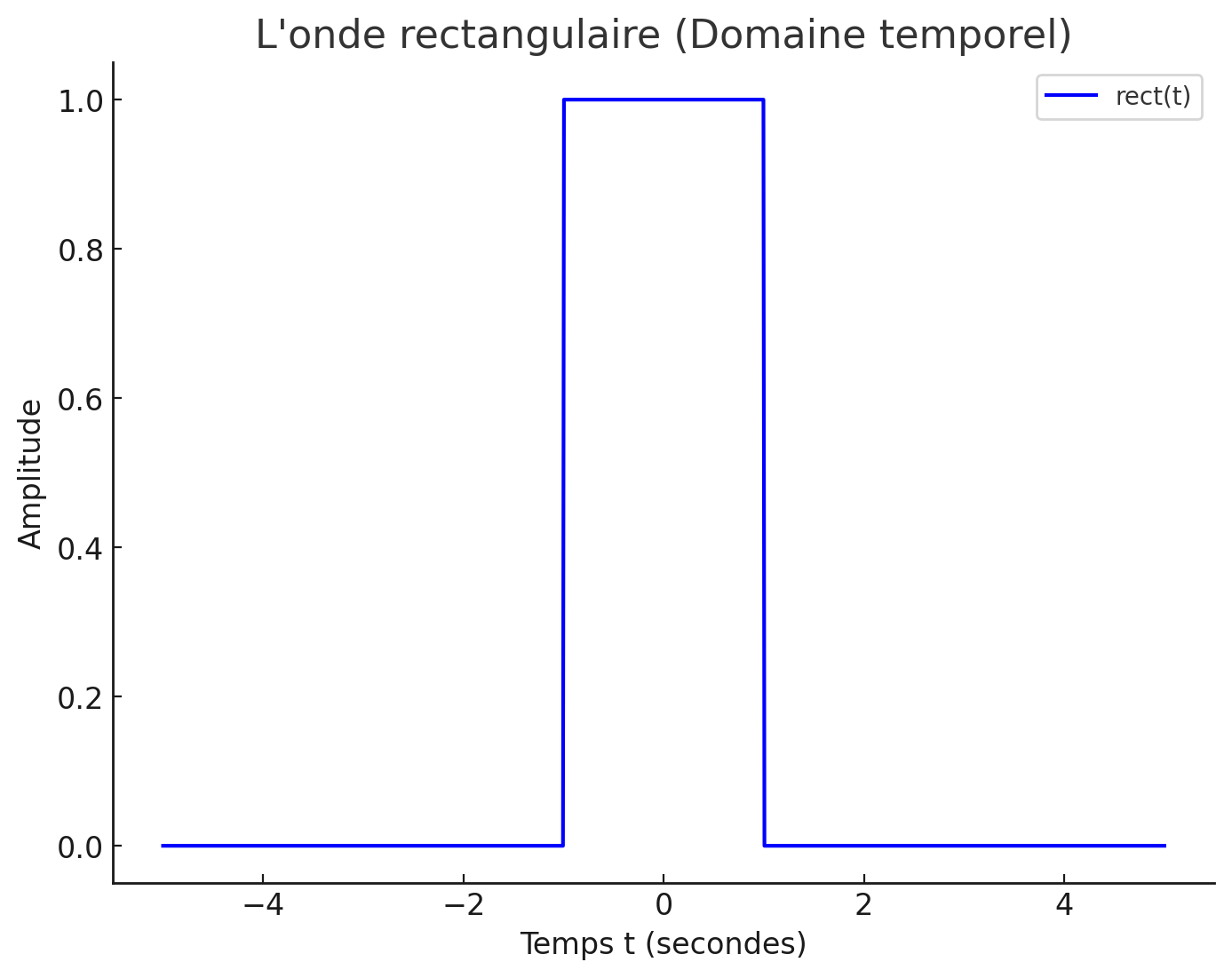
Figure 14:Onde rectangulaire (en domaine fréquentiel).
Propriétés:
La valeur moyenne :
L’énergie :
La puissance :
La transformée de Fourier :
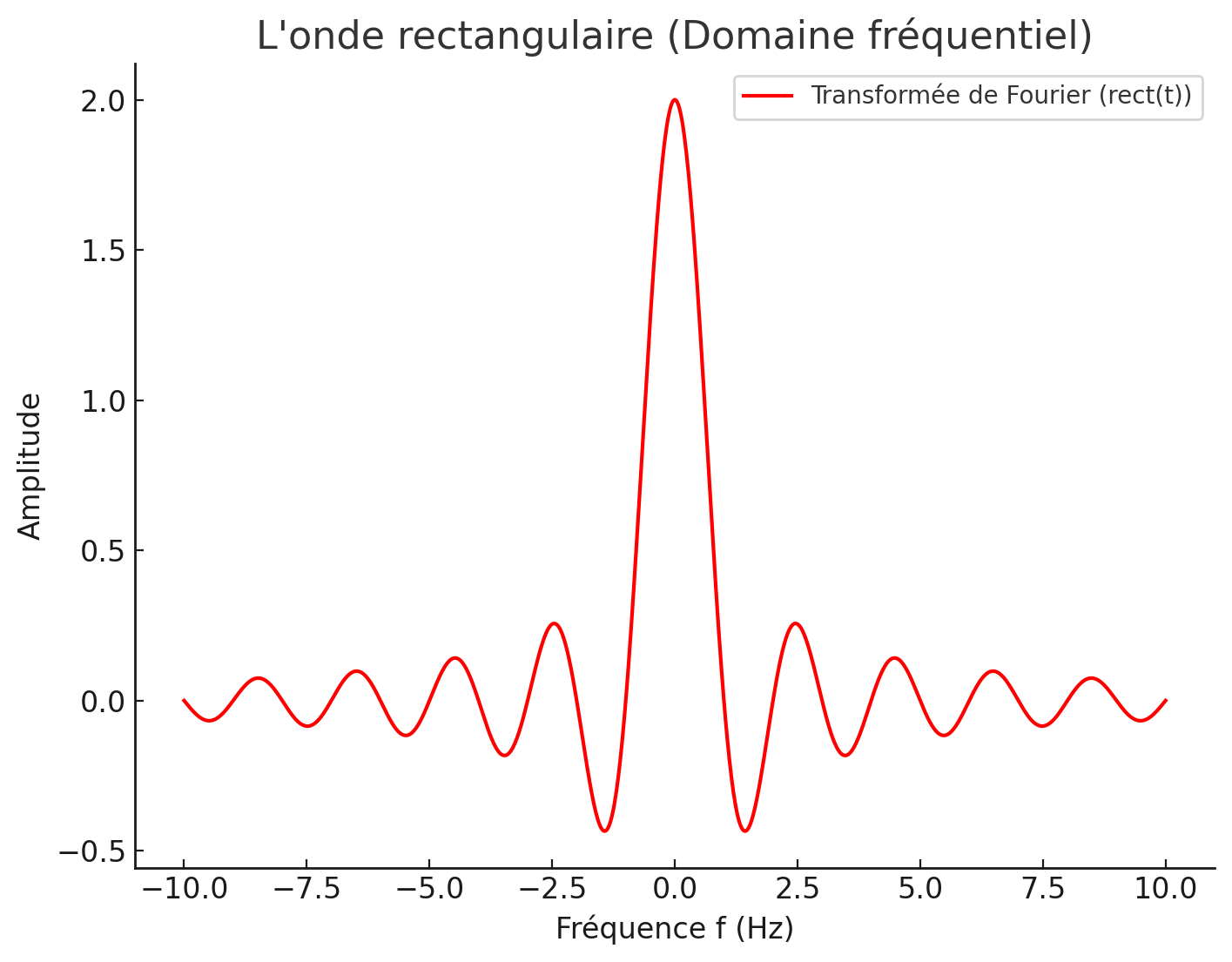
Figure 15:Onde rectangulaire (en domaine temporel).
Ondes porteuses (Carrier waveforms)¶
- Définition: Ondes porteuses
- La majorité des systèmes de communication utilisent les formes d’onde cosinus et sinus comme ondes porteuses. Leur fréquence fondamentale est appelée la fréquence porteuse.
Un cosinus avec fréquence et amplitude est défini comme où :
est l’amplitude,
est la fréquence en Hertz,
ϕ est la phase initiale (en radians),
est le temps.
Propriétés:
La valeur moyenne :
L’énergie : infinie
La puissance :
La transformée de Fourier :
Pour un sinus avec les mêmes paramètres
Propriétés:
La valeur moyenne : 0
L’énergie : infinie
La puissance :
La transformée de Fourier :
Système¶
- Définition: Système
- Du point de vue d’un ingénieur en communication, un système est une loi qui attribue des signaux de sortie à divers signaux d’entrée.
Le point le plus important dans la définition d’un système est que sa sortie doit être définie de manière unique pour toutes les entrées légitimes.
Chaque système possède une entrée () une sortie et une fonction de transfert , ou .
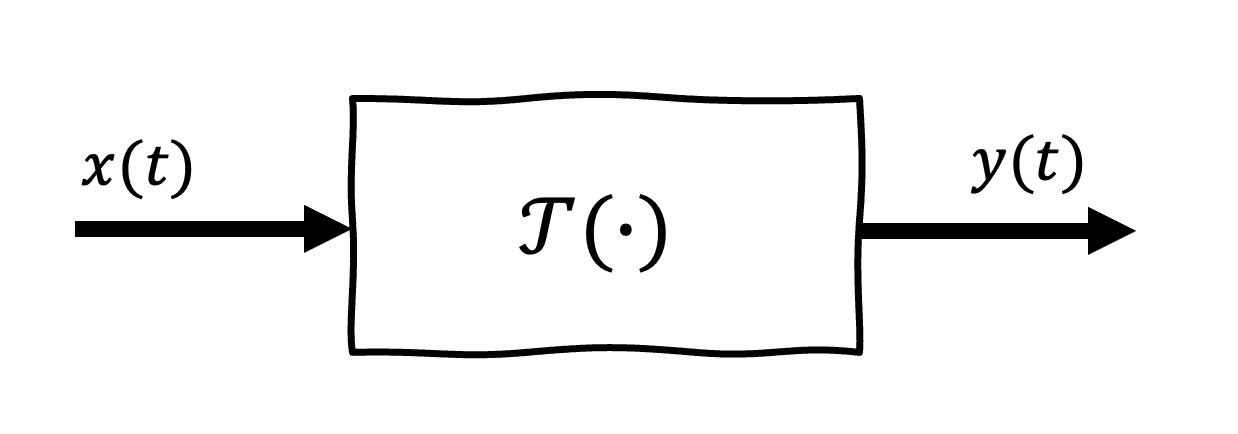
Figure 1:Représentation d`un système
Catégories de systèmes¶
Un système peut être variant ou invariant dans le temps. De plus, un système peut être linéaire ou non linéaire. Leurs explications sont données ci-dessous.
Système invariant dans le temps (Time Invariant System)¶
Un système est invariant dans le temps si sa réponse à une entrée ne change pas lorsque l’entrée est décalée dans le temps. Si l’on considère un système avec une entrée et une sortie , (i.e. ), le système est invariant dans le temps si
Système variant dans le temps (Time Varying System)¶
Le système est variant dans le temps quand l’équation (49) n’est pas applicable.
Système linéaire (Linear System)¶
Un système est linéaire s’il respecte les propriétés suivantes :
homogénéité : si une entrée produit une sortie , i.e.,, la sortie de pour un scalaire produit .
superposition : si un signal est composé de plusieurs composantes, telles que
où , ,
Notez que la transformée de Fourier peut être interprétée comme un système linéaire.
Système linéaire invariant dans le temps (Linear time invariant; LTI)¶
Un système est linéaire invariant dans le temps (LTI) si les propriétés de linéarité et d’invariance dans le temps sont satisfaites. Ce système est défini simplement par sa réponse impulsionnelle, , ou sa réponse fréquentielle où
.
La sortie est obtenue par la convolution de l’entrée avec la réponse impulsionnelle où
.
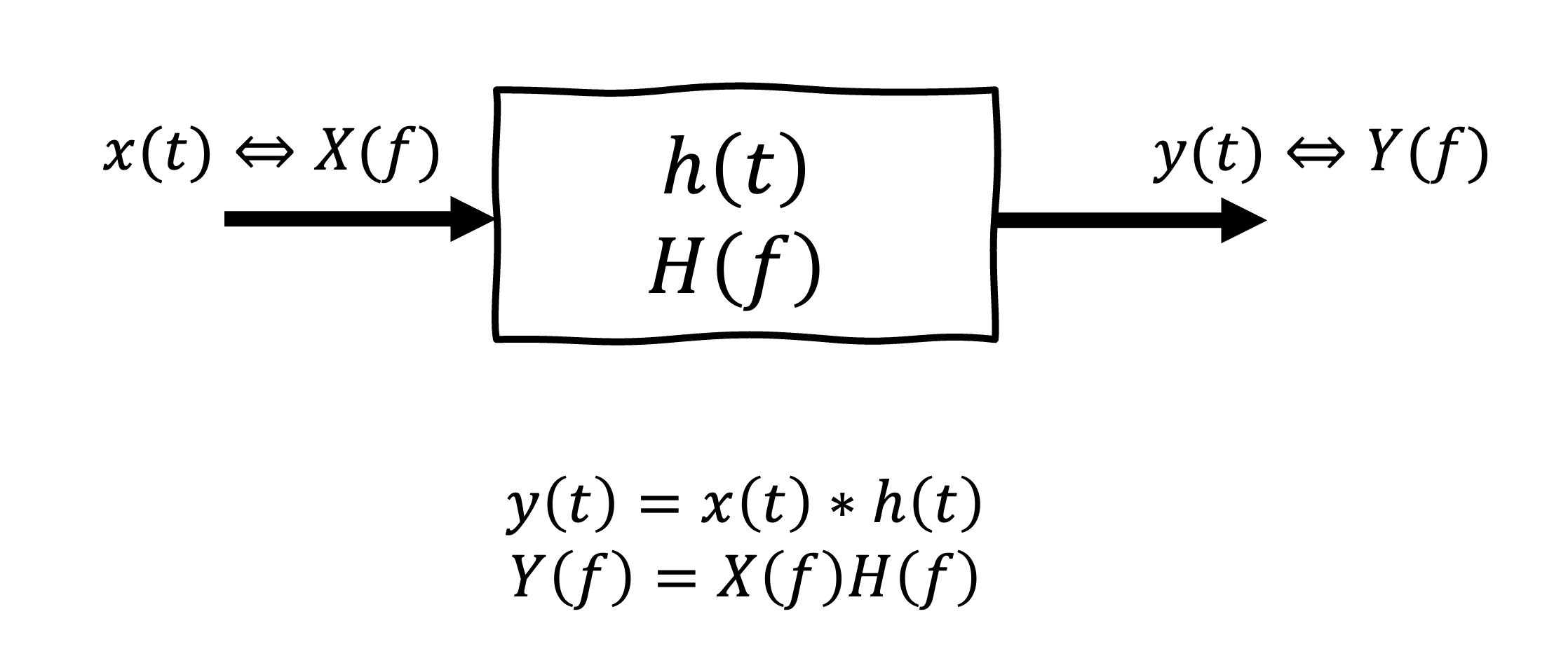
Figure 17:Transmission d’un signal à travers un système linéaire invariant dans le temps (LTI)
Système non linéaire (Nonlinear System)¶
Si un système ne respecte pas l’une ou l’autre des propriétés d’homogénéité ou de superposition, il est non linéaire.Leur réponse peut varier de manière non proportionnelle ou non additive en fonction des entrées.
Modulation - un système non linéaire¶
La modulation est le processus par lequel une onde portesue est multiplié par un signal de message . Cela permet d’intégrer l’information du message dans une onde porteuse adaptée à la transmission.
Pour une modulation d’amplitude (AM), le signal modulé s’écrit :
où est l’amplitude de la porteuse et sa fréquence.
Dans ce cas, le signal d’information module l’amplitude de l’onde porteuse . Soit a un largeur de bande Hz avec une réponse fréquentielle . La reponse fréquentielle du signal modulé sera
Donc la largeur de bande du signal modulé est de Hz.
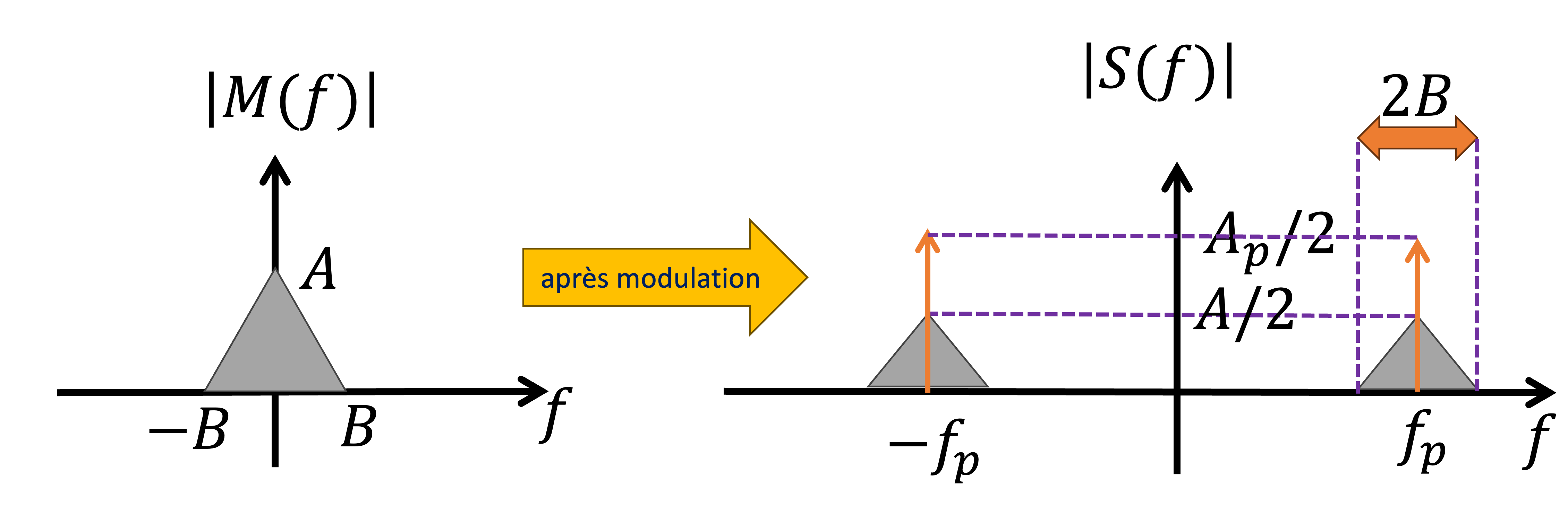
Figure 18:Une illustration de la modification de la largeur de bande et de l’amplitude
Probabilité¶
Probabilité et la règle de Bayes¶
Les définitions ci-dessous forment la base de la théorie des probabilités, utilisée dans de nombreux domaines comme les statistiques, l’apprentissage automatique et les communications. Elles permettent de quantifier les incertitudes et d’effectuer des prédictions basées sur des observations. Nous les utiliserons principalement pour calculer l’énergie et la puissance des signaux.
Soit le nombre total d’événements dans un espace d’échantillonnage. Les notions clés associées à la probabilité sont expliquées ci-dessous :
Un événement correspond à un ensemble d’issues spécifiques parmi les issues possibles. Le nombre de fois où l’événement se réalise est noté comme , qui indique la réalisation de .
La probabilité d’un événement est définie comme la limite, lorsque tend vers l’infini, du rapport entre et :
avec
Cela signifie que la probabilité est une mesure entre 0 et 1 de la fréquence relative de réalisation de .
La probabilité conditionnelle de sachant que est réalisé est donnée par :
où représente la probabilité de la conjonction des événements et , et .
La règle de Bayes nous permet de calculer la probabilité conditionnelle de sachant en inversant la condition :
Cette règle est particulièrement utile dans les problèmes où il est plus facile de calculer que directement.
Variables aléatoires¶
Une variable aléatoire nous permet de modéliser des événements aléatoires avec une règle d’association de valeurs. La fonction de distribution cumulative est un outil clé pour analyser les probabilités associées à ces variables, en respectant des propriétés fondamentales comme la continuité et la monotonie.
- Définition: Variable aléatoire
- Une variable aléatoire résulte de l’application d’une règle par laquelle une valeur est assignée à un événement.
- Définition: Fonction de distribution cumulative
- Fonction de distribution cumulative (Cumulative Distribution Function; CDF)} La fonction de distribution cumulative (ou CDF, pour Cumulative Distribution Function) est définie comme : où représente la probabilité que la variable aléatoire soit inférieure ou égale à une valeur donnée .
Propriétés :
, pour tout .
.
.
, pour (c’est-à-dire, est une fonction non décroissante).
- Définition: Fonction de densité de probabilité
- La fonction de densité de probabilité (Probability Density Function; PDF) caractérise la distribution des probabilités pour une variable aléatoire continue. La PDF d’une variable aléatoire est définie comme étant la dérivée de la fonction de distribution cumulative (CDF) :
Propriétés :
, pour tout .
L’intégrale de sur tout l’espace est égale à 1 :
La CDF peut être exprimée comme l’intégrale de la PDF :
Les moyennes statistiques¶
Les moyennes statistiques sont des outils fondamentaux pour décrire et analyser les propriétés d’une variable aléatoire. Ces outils sont essentiels pour caractériser le comportement statistique des systèmes aléatoires.
La valeur moyenne (ou espérance ) d’une variable aléatoire est donnée par :
où représente l’espérance de , est sa PDF. Cette moyenne représente la valeur centrale attendue de .
Si une fonction est appliquée à une variable aléatoire , la moyenne de cette fonction est donnée par :
Cela permet de calculer l’espérance de transformations non linéaires de .
La variance mesure la dispersion d’une variable aléatoire autour de sa moyenne. Elle est définie par :
où est la variance de , et est la valeur moyenne de .
Puissance d’une variable aléatoire¶
La puissance d’une variable aléatoire , définie comme
Distribution gaussienne (normal)¶
La distribution gaussienne (ou loi normale) est l’une des distributions les plus importantes en probabilité et statistiques.
Propriétés :
- Fonction de densité de probabilité (PDF) d’une variable aléatoire suivant une distribution gaussienne est donnée par : où μ est la moyenne (ou valeur moyenne) de la distribution, est la variance, et σ est l’écart type (standard deviation).
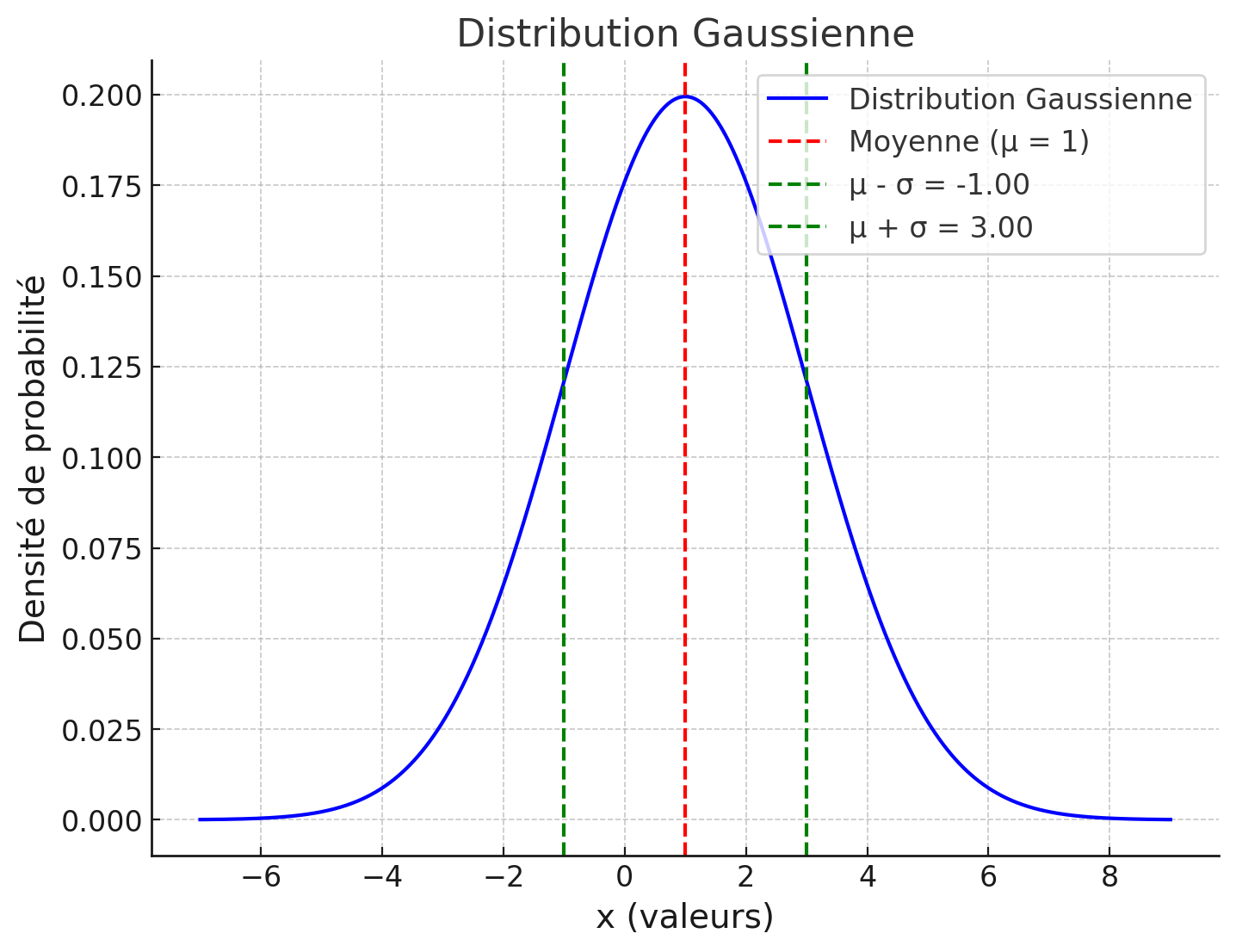
Figure 19:Une distribution gaussienne avec une moyenne μ et une variance .
- Pour une variable aléatoire suivant une distribution gaussienne, la probabilité que soit supérieure à une valeur : où est la fonction Q, définie par :
- La probabilité que soit inférieure ou égale à une valeur :
Signaux aléatoires¶
- Définition: Signal aléatoire
- Un signal aléatoire est une réalisation particulière ou une trajectoire d’un processus aléatoire.
- Définition: Processus aléatoire
- Un processus aléatoire peut être défini simplement comme un ensemble de variables aléatoires. On dit d’un processus aléatoire qu’il est stationnaire au sens strict lorsque les moyennes statistiques d’ensemble ne changent pas dans le temps. Lorsqu’on ne considère que les deux premiers moments, on parlera de stationnarité au sens large.
Un processus aléatoire est ergodique lorsque les moyennes statistiques d’ensemble sont égales aux moyennes statistiques dans le temps de chacune des variables qui le composent.
Autocorrélation¶
L’autocorrélation d’un processus aléatoire mesure la similitude entre les valeurs du processus à deux instants différents, séparés par un décalage τ. Pour le décalage temporel τ, elle est définie par l’expression suivante :
Cette équation analyse la corrélation temporelle des valeurs du processus.
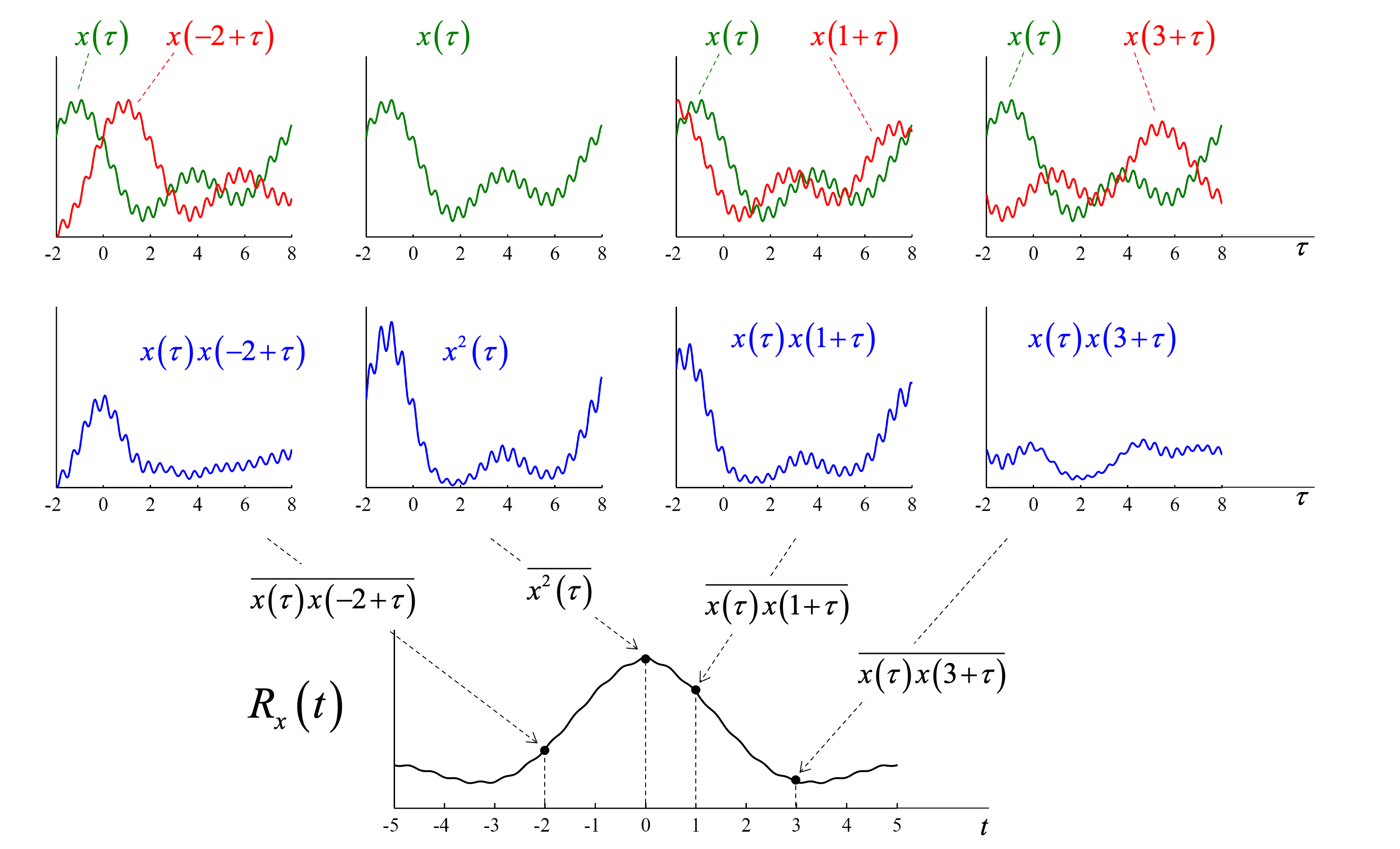
Figure 20:Une illustration de l’autocorrélation d’une réalisation d’un signal aléatoire
Spectre de densité de puissance¶
Le spectre de densité de puissance (power spectral density; PSD) est un outil clé pour analyser la répartition de la puissance d’un signal dans le domaine fréquentiel.
La puissance moyenne d’un signal aléatore peut être exprimée e à l’aide de la fonction de densité de puissance , définie comme :
où est le spectre de densité de puissance obtenu en prenant la limite lorsque . Notez que représente la densité spectrale de puissance.
La puissance moyenne du signal dans une bande de fréquence spécifique est donnée par :
![Une illustration de la puissance moyenne du signal dans la bande [f_1, f_2]](/build/psd-3e8e13aa1a459530cc02d87bd7cbe556.png)
Figure 20:Une illustration de la puissance moyenne du signal dans la bande
Relation entre autocorrélation et spectre de densité de puissance¶
L’autocorrélation et le spectre de densité de puissance d’un signal aléatoire sont reliés par une transformée de Fourier :
où est la fonction d’autocorrélation dans le domaine temporel et est le spectre de densité de puissance dans le domaine fréquentiel.
Cette relation signifie que :
- La transformée de Fourier de la fonction d’autocorrélation donne le spectre de densité de puissance.
- La transformée inverse du spectre de densité de puissance donne la fonction d’autocorrélation.
Filtrage d’un signal aléatoire¶
Lorsqu’un signal aléatoire traverse un système linéaire invariant dans le temps (LTI), le comportement du signal en sortie peut être analysé à l’aide des propriétés du système, caractérisé par sa réponse impulsionnelle ou sa réponse fréquentielle .
Soit le spectre de densité de puissance d’entrée représenté par , et le système est caractérisé par , la réponse impulsionnelle (ou , la réponse fréquentielle)
Le spectre de densité de puissance en sortie est donné par :
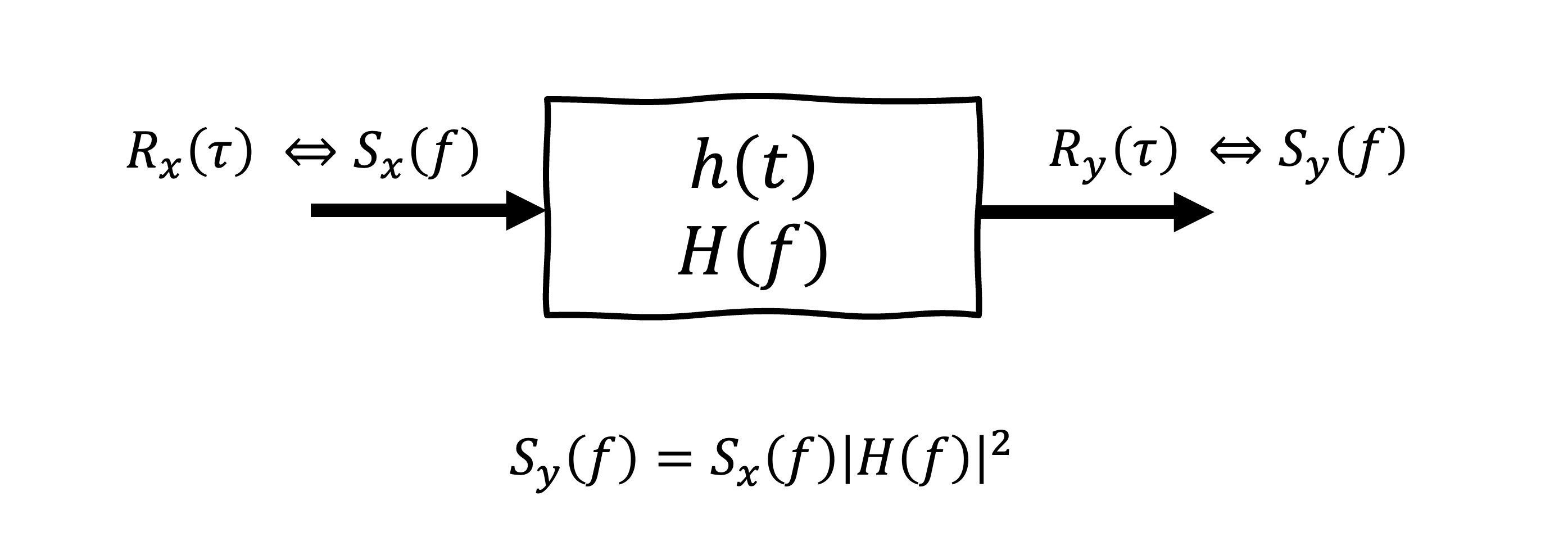
Figure 22:La sortie d’un système LTI pour une entrée avec un spectre de densité de puissance de .
Resumé¶
Dans cette section, nous abordons O2 application des outils d’analyse spectrale pour résoudre des problèmes liés aux procédures de transmission. L’analyse spectrale joue un rôle fondamental dans la conception et l’optimisation des systèmes de communication. En représentant les signaux dans le domaine fréquentiel, les ingénieur.e.s peuvent mieux comprendre le contenu spectral et le comportement des signaux transmis. Cette approche facilite l’identification des éléments essentiels tels que la bande passante, la distribution de puissance et le contenu fréquentiel. Les outils spectraux permettent également de concevoir des filtres efficaces pour éliminer les fréquences indésirables, allouer les ressources de manière optimale et réduire les interferences. Ces techniques sont indispensables pour garantir une transmission fiable et efficace des signaux dans les réseaux de communication modernes.