Abstract¶
Section 5 aborde les phénomènes liés à la distorsion et au canal de transmission. Tout d’abord, elle traite de la distorsion, distinguant clairement la distorsion dans les systèmes linéaires de la distorsion non linéaire. Ensuite, la section examine le canal de transmission en introduisant la limite de Shannon, une frontière théorique définissant la capacité maximale de transmission sans erreurs pour un canal donné. Des exemples pratiques de modèles physiques de canaux sont également présentés pour illustrer ces concepts théoriques. Par la suite, la section détaille le modèle statistique du canal, essentiel à l’analyse de performance des systèmes de communication. Elle présente notamment le modèle de canal binaire, largement utilisé pour quantifier les performances d’un canal en termes de taux d’erreur binaire. L’objectif O5 est ainsi de comprendre et d’analyser les différentes formes de distorsion ainsi que les caractéristiques des canaux de transmission afin de pouvoir évaluer leur impact sur les performances des systèmes de communication et mettre en place les solutions adaptées pour minimiser les erreurs.
Introduction¶
Un canal de transmission est le support permettant la transmission d’un signal entre un émetteur et un récepteur dans un système de communication. Ce canal peut être un médium physique, tel qu’un câble ou une fibre optique, ou encore un médium sans fil comme l’air ou l’espace. Quelle que soit sa nature, le canal influence le signal transmis en introduisant divers phénomènes perturbateurs, tels que du bruit, des interférences et de la distorsion.
Distorsion¶
Les effets du canal (distortion) peuvent être regroupés en deux catégories principales : les effets linéaires et non linéaires. La distortion linéaire inclue l’atténuation, où la puissance du signal diminue avec la distance ou la nature du canal, la dispersion, provoquant l’étalement du signal dans le temps ou en fréquence, et la propagation par trajets multiples (multi-trajet), générant des interférences dues à la réflexion et à la diffraction des ondes. Ces phénomènes sont généralement modélisables par des équations linéaires et traités par des outils mathématiques comme la convolution ou l’analyse fréquentielle (donc les effets linéairessont modélisés comme un système linéaire, en utilisant une réponse impulsionnelle (ou une réponse fréquentielle)).
En revanche, la distortion non linéaire provient d’une relation non proportionnelle entre l’entrée et la sortie du canal, souvent causée par les composants électroniques tels que les amplificateurs. Ces effets ne peuvent pas simplement être modélisés comme un filtre ; la sortie doit donc être caractérisée en fonction de la réponse du système à chaque entrée spécifique. Parmi ces effets figurent les distorsions harmoniques et d’intermodulation, qui créent des fréquences parasites indésirables et plus complexes à gérer.
L’objectif principal de l’introduction de modèles mathématiques est de quantifier précisément les effets du canal sur les ressources du système de communication, notamment la puissance du signal et la bande passante disponible. Grâce à ces modèles, il devient possible d’optimiser les ressources, d’améliorer la robustesse des systèmes de communication face aux imperfections du canal, et de déterminer les limites théoriques de performance comme définies par la capacité de Shannon.
Distorsion linéaire¶
Nous présentons ici un modèle mathématique décrivant la distorsion linéaire. Le signal de message est d’abord modulé sur une onde porteuse, donnant naissance au signal transmis . Ce dernier traverse ensuite un canal caractérisé par une réponse impulsionnelle (ou sa réponse fréquentielle associée ). À la sortie du canal, le signal reçu subit l’ajout d’un bruit thermique , générant ainsi le signal perturbé avant sa démodulation.
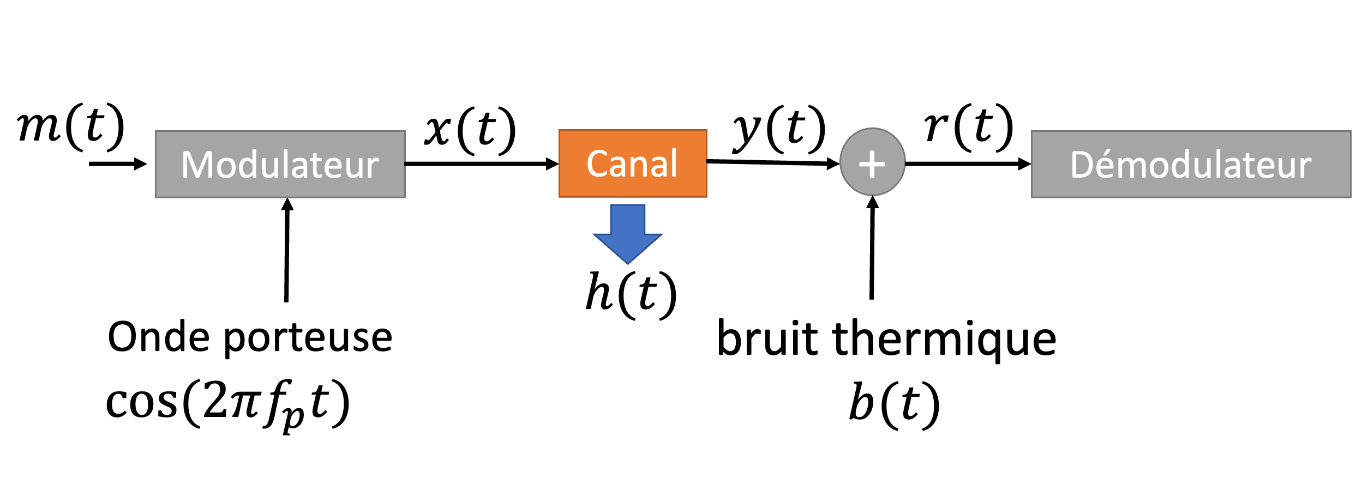
Figure 5:Schéma d’une transmission linéaire avec modulation, caractérisant l’effet du canal par sa réponse impulsionnelle et l’ajout d’un bruit thermique.
Nous pouvons chercher à identifier l’impact de la distorsion à l’aide des harmoniques. Un harmonique désigne une composante fréquentielle d’un signal périodique, dont la fréquence est un multiple entier de la fréquence fondamentale du signal initial. Par exemple, si un signal possède une fréquence fondamentale (ou première harmonique), les harmoniques suivantes (2ème, 3ème, 4ème, etc.) auront des fréquences égales à deux, trois, quatre fois ou plus cette fréquence fondamentale.
Dans un signal complexe, les harmoniques jouent un rôle essentiel dans la forme finale du signal. La manière dont les harmoniques s’additionnent influence fortement la forme d’onde résultante. Ainsi, si l’amplitude d’un harmonique augmente significativement, ou si sa phase se décale, le signal total peut subir des modifications notables, entraînant une distorsion non linéaire. Par conséquent, le contrôle précis des amplitudes et des phases des harmoniques est crucial pour préserver l’intégrité du signal transmis dans les systèmes de communication.
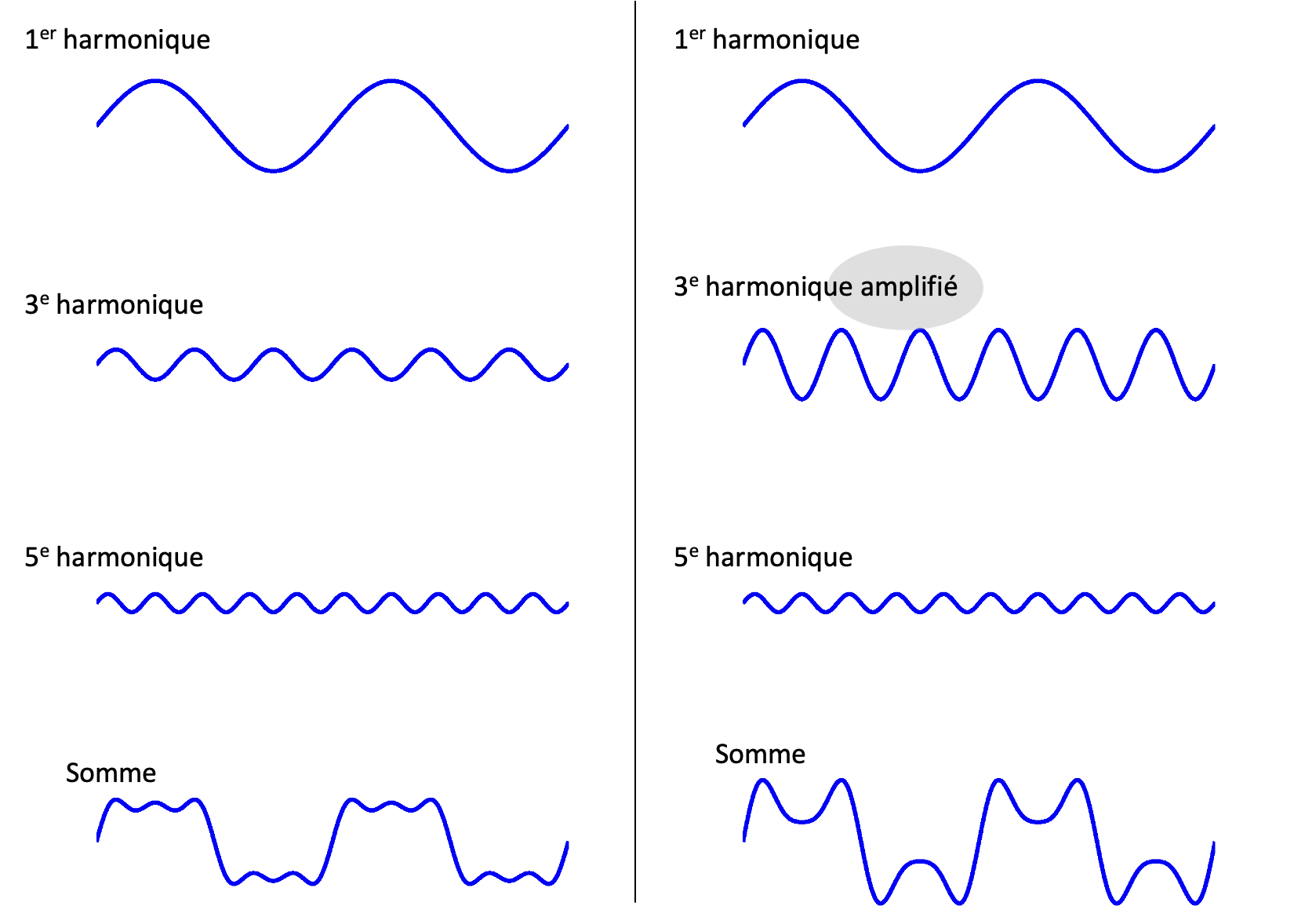
Figure 6:Illustration de la distorsion non linéaire par modification de l’amplitude des harmoniques.
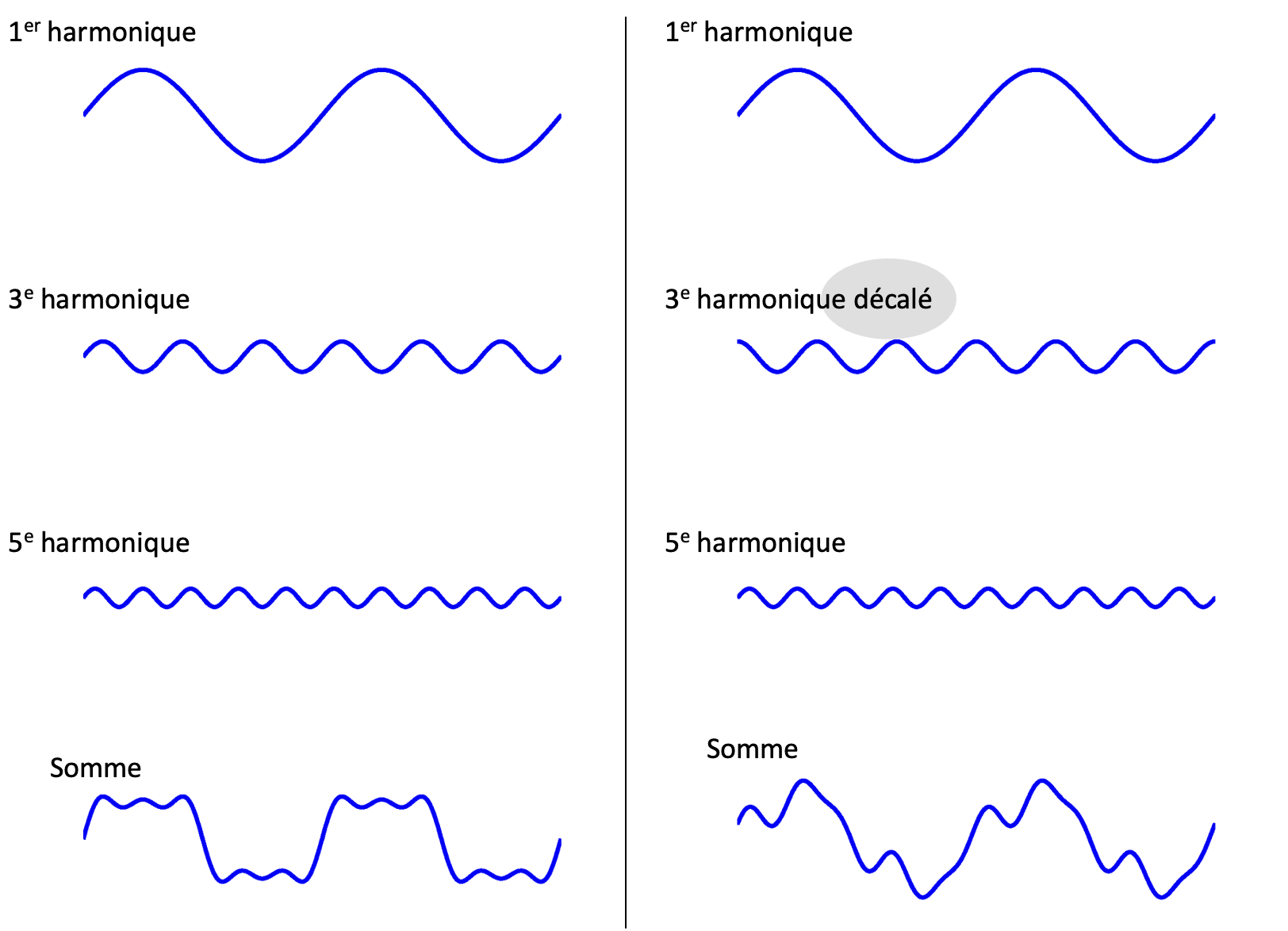
Figure 7:Illustration de la distorsion non linéaire par modification de la phase des harmoniques.
Distorsion non linéaire¶
La distorsion harmonique aussi apparaît lorsqu’un signal traverse un système non linéaire, où la réponse du système n’est pas directement proportionnelle à l’entrée.

Figure 8:Représentation simplifiée d’un système non linéaire caractérisé par une relation entrée-sortie.
En pratique, l’analyse de la distorsion harmonique se fait en considérant spécifiquement la réponse du système pour chaque entrée donnée. Cela signifie que la forme et l’amplitude des harmoniques générées dépendent directement à la fois des caractéristiques intrinsèques du système étudié (sa réponse non linéaire) et de la nature exacte du signal d’entrée. Par conséquent, il est essentiel d’effectuer cette analyse au cas par cas, pour déterminer précisément comment la combinaison système-entrée affecte la qualité et l’intégrité du signal transmis.
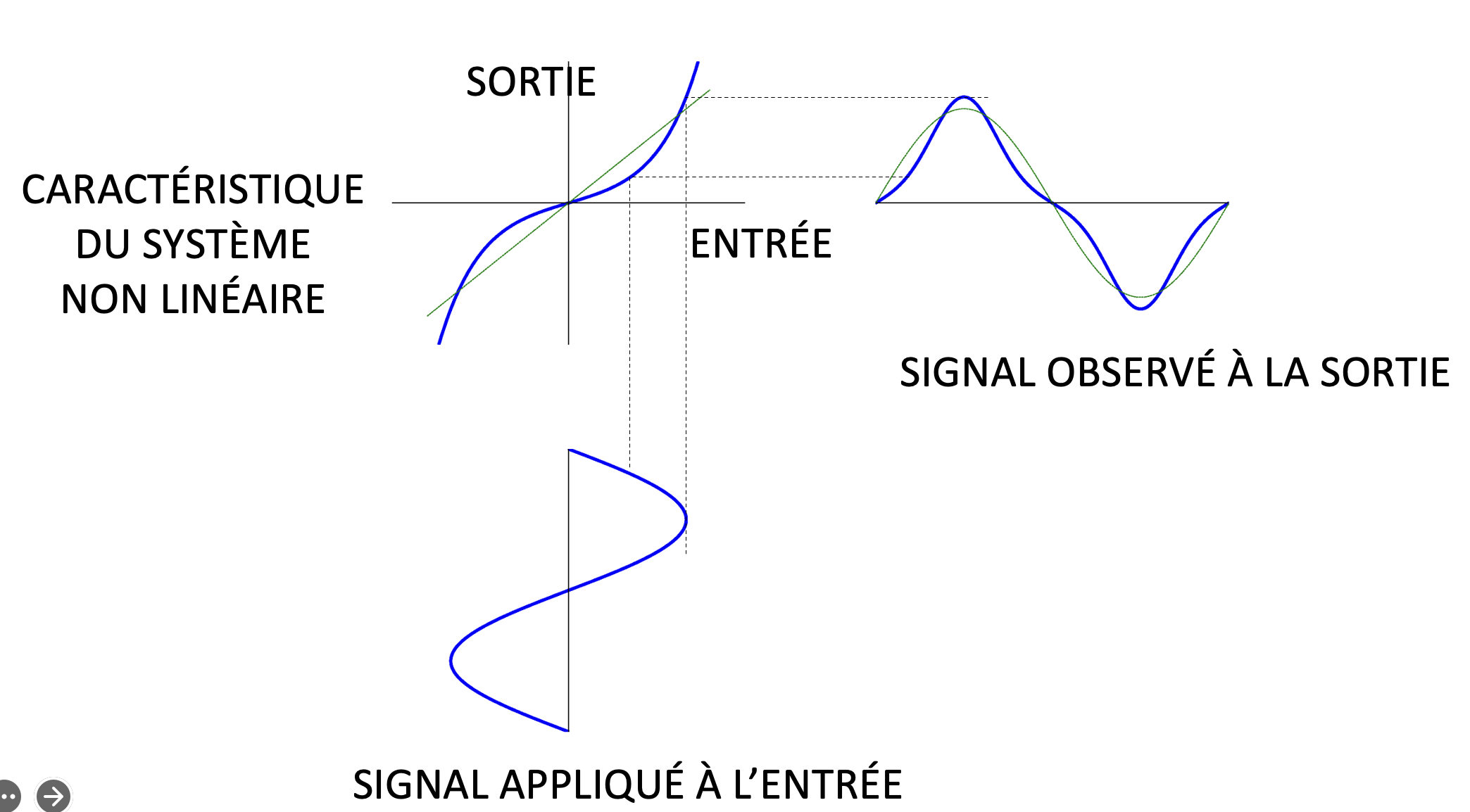
Figure 9:Illustration graphique de la distorsion harmonique générée par la réponse non linéaire d’un système à un signal sinusoïdal en entrée. Un signal sinusoïdal appliqué à l’entrée subit une déformation lorsqu’il traverse le système, en raison de la relation non linéaire entre l’entrée et la sortie. La courbe représentant cette relation (caractéristique du système non linéaire) montre clairement une déviation par rapport à la linéarité. Ainsi, le signal obtenu à la sortie est modifié, présentant une forme d’onde différente de celle du signal d’entrée initial, caractéristique de la distorsion harmonique.
Canal de transmission¶
La transmission d’un signal numérique à travers un canal est modélisé comme un filtre passe-bas. Le signal numérique, caractérisé par un débit de bits bits par seconde, traverse le canal ayant une bande passante disponible de Hz. À la sortie du canal, le signal reçu est perturbé par un bruit thermique , ce qui génère le signal résultant envoyé au démodulateur.
La capacité maximale du canal (en bits par seconde) est donnée par la célèbre formule de Claude Shannon :
Cette formule exprime la capacité maximale théorique (débit maximal sans erreurs possible) d’un canal de bande passante Hz, en fonction du rapport signal à bruit (SNR), représenté par le rapport entre la puissance moyenne du signal, , et la puissance moyenne du bruit, . En pratique, cette équation indique que pour augmenter la capacité, il est possible d’accroître la bande passante disponible ou d’améliorer le rapport signal à bruit, c’est-à-dire en augmentant la puissance du signal ou en réduisant le niveau de bruit. La capacité calculée par cette formule est une limite théorique fondamentale, non dépassable, quel que soit le codage utilisé.
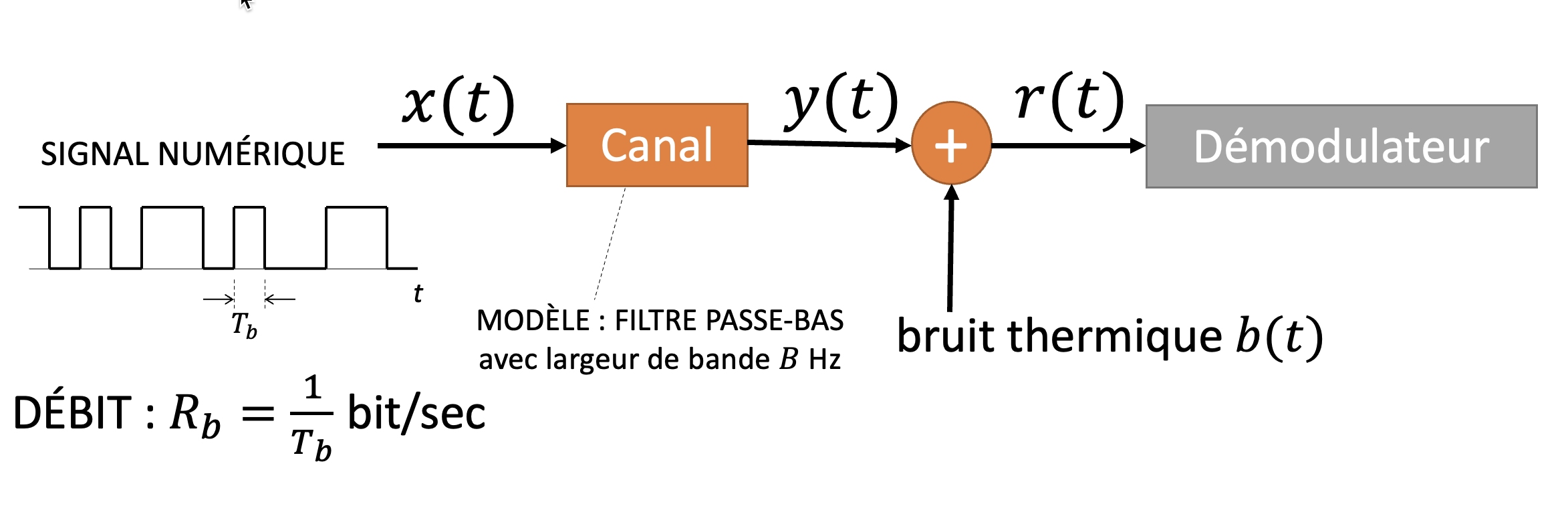
Figure 10:Transmission numérique à travers un canal bruité et limite théorique de capacité selon la formule de Shannon.
Modèle statistique du canal¶
Un modèle simplifié de canal binaire, est utilisé pour étudier la transmission d’une information binaire ( ou ) à travers un canal de communication potentiellement bruité. Dans ce modèle, l’information émise (notée ( E )) peut prendre deux valeurs possibles : ou . La décision prise à la réception (notée ( D )) peut également être ou .
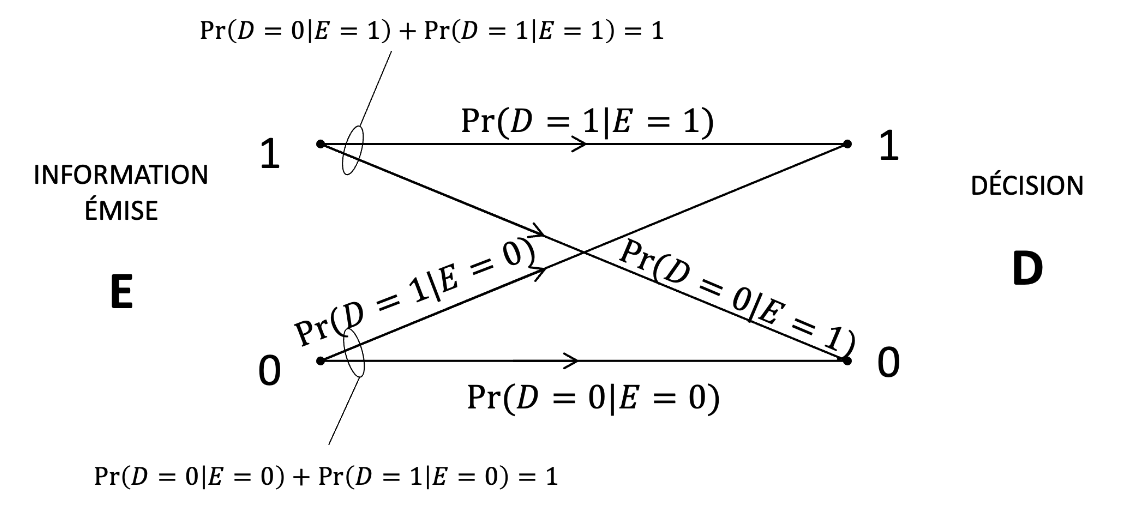
Figure 11:Modèle statistique d’un canal binaire présentant les probabilités de décisions correctes et erronées.
Les paramètres représentés sont les probabilités conditionnelles :
- : Probabilité que la décision soit correcte ( reçu sachant que a été envoyé).
- : Probabilité que la décision soit correcte ( reçu sachant que a été envoyé).
- : Probabilité d’erreur, décidant alors que était envoyé.
- : Probabilité d’erreur, décidant alors que était envoyé.
Les relations suivantes sont vérifiées :
Ces probabilités permettent de caractériser précisément la performance du canal en termes de fiabilité et de taux d’erreur binaire.
La probabilité d’erreur moyenne pour un canal binaire décrit la probabilité qu’un bit transmis soit incorrectement reçu. Elle est définie par :La probabilité d’erreur moyenne pour un canal binaire décrit la probabilité qu’un bit transmis soit incorrectement reçu. Elle est définie par :
En développant cette expression à l’aide des probabilités conditionnelles, on obtient :
Resumé¶
Cette section traite de O5. Modélisation d’un canal de transmission et explication des imperfections associées. Elle explore les différents supports de transmission, incluant les canaux physiques (paire torsadée, câble coaxial, fibre optique) et sans fil, ainsi que les effets des canaux tels que la distorsion linéaire (atténuation, dispersion, trajets multiples) et non linéaire (distorsions harmonique et d’intermodulation). Un accent particulier est mis sur les modèles mathématiques permettant de caractériser ces effets, notamment à travers l’analyse fréquentielle et l’étude des harmoniques. La formule de Shannon est introduite pour illustrer la limite théorique de capacité d’un canal, soulignant l’importance du rapport signal-bruit et de la bande passante disponible.