Section 6 - Contrôle des erreurs

Abstract¶

Cette section traite des techniques de codage utilisées pour détecter et corriger les erreurs dans les systèmes de communication numériques. Elle aborde les catégories de codes, les fondements théoriques du codage, ainsi que les différences entre les codes blocs et les codes convolutionnels. Le but est de comprendre comment ces mécanismes assurent l’intégrité des données transmises, malgré les imperfections du canal de communication. L’objectif est de savoir appliquer les techniques de codage pour améliorer la fiabilité d’un lien de transmission.

Introduction¶

Le codage pour le contrôle des erreurs est utilisé dans les systèmes de communication numériques pour garantir une transmission fiable des données malgré les perturbations du canal. Les données d’entrée, sous forme numérique (binaire), sont encodées en mots de code contenant des bits redondants qui permettent de détecter et corriger les erreurs. Ces systèmes (comme les codes blocs ou convolutionnels) jouent un rôle essentiel dans les applications telles que les réseaux sans fil, les systèmes de stockage ou les transmissions par satellite, réduisant ainsi les pertes de données et améliorant l’efficacité globale.

Le contrôle des erreurs est une composante essentielle des systèmes de communication modernes. Sa cible principale est de garantir une transmission fiable des données malgré les imperfections des canaux de communication, tels que le bruit, les interférences ou les pertes de signal. En introduisant des mécanismes de détection et de correction des erreurs, le contrôle des erreurs permet d’assurer l’intégrité des données tout en minimisant le besoin de retransmissions.

Théorie du Codage¶

Le codage joue un rôle fondamental dans les systèmes de communication en structurant les données de manière à faciliter la détection et la correction des erreurs.

Les canaux de communication sont souvent imparfaits , ce qui introduit des erreurs dans les données transmises (comme nous l’avons vu dans la section 5). Ces erreurs peuvent provenir de diverses sources, notamment le bruit thermique, les interférences et les limitations physiques.

L’objectif du codage de canal est de transmettre des bits redondants pour permettre au récepteur la détection et/ou la correction d’erreur de transmission. L’information numérique (en bits) est d’abord transformée en un mot de code par l’émetteur, puis transmise à travers un canal de communication. Ce canal est modélisé comme étant affecté par un bruit thermique, ce qui peut altérer le mot de code pendant la transmission. Le récepteur reçoit alors une version potentiellement erronée du message et doit prendre une décision sur l’information transmise. Cependant, comme aucun mécanisme de codage n’a été mis en place pour insérer de la redondance et permettre la détection ou la correction d’erreurs, le système ne dispose d’aucun moyen pour vérifier l’intégrité des données reçues.

Figure 1:Chaîne de transmission sans codage de canal : sans redondance ajoutée par un code correcteur, le récepteur ne peut pas détecter les erreurs causées par le bruit du canal.

Les codes de contrôle des erreurs peuvent être classés en deux catégories principales; les codes blocs, et les codes convolutionnels.

Les codes blocs transforment des blocs fixes de données en mots de code plus longs, ajoutant une redondance pour détecter et corriger les erreurs. Les codes de bloc fonctionnent en divisant les données en blocs de $k$ bits, puis en les encodant en mots de code plus longs composés de $n$ bits, où $n > k$ . Chaque bloc de données produit ainsi un mot de code unique, permettant d’introduire de la redondance pour la détection et la correction d’erreurs.

En revanche, les codes convolutionnels génèrent des mots de code où chaque séquence codée dépend non seulement des bits actuels ( $k$ ), mais aussi d’un certain nombre de bits précédents ( $N - 1$ ). Cela permet une protection plus continue contre les erreurs, particulièrement efficace dans les transmissions longues ou en flux continu. Ces deux approches constituent les fondements du codage de canal.

Contrairement aux codes blocs, les codes convolutionnels : génèrent des mots de code basés sur les bits actuels et précédents, ce qui offre une protection continue. Dans ce cours, nous nous concentrerons sur les types fondamentaux de codes blocs, tandis que les codes convolutionnels seront introduits pour offrir un aperçu complémentaire du sujet.

Définitions requises¶

Pour pouvoir utiliser les opérations binaires, nous avons besoin de quelques définitions.

Définition: Champs de Galois (Galois field): Les calculs dans le codage reposent souvent sur des champs de Galois (Galois field; GF), tels que GF(2). Ces champs permettent de définir des opérations binaires, comme l’addition et la multiplication modulo 2, qui sont au cœur des algorithmes de codage.

Les opérations dans le champ de Galois GF(2) sont essentielles pour le codage et le décodage dans les systèmes numériques. Voici les deux opérations fondamentales :

Définition: Addition modulo 2

L’addition dans GF(2) est équivalente à l’opération XOR (ou exclusif) entre deux bits. Cette opération est commutative et associative.

Règles :

$\texttt{0} \oplus \texttt{0 = 0}$ ,
$\texttt{1} \oplus \texttt{1 = 0}$ ,
$\texttt{0} \oplus \texttt{1 = 1}$ ,
$\texttt{1} \oplus \texttt{0 = 1}$ .

Notez que toute valeur ajoutée à elle-même donne $\texttt{0}$ , ( $\texttt{ a }\oplus \texttt{ a = 0}$ ).

Définition: Multiplication modulo 2

La multiplication dans GF(2) est équivalente à l’opération AND logique entre deux bits. Elle est également commutative et associative.

Règles :

$\texttt{0 x 0 = 0}$ ,
$\texttt{1 x 1 = 1}$ ,
$\texttt{0 x 1 = 0}$ ,
$\texttt{1 x 0 = 0}$ .

Notez que toute valeur multipliée par $\texttt{0}$ , donne $\texttt{0}$ ,, et par $\texttt{1}$ , donne elle-même ( $\texttt{ a x 1 = a}$ ).

Définition: Poids de Hamming (Hamming weight): Le poids de Hamming d’un mot de code est défini comme le nombre de bits égaux à $\texttt{1}$ dans ce mot. C’est une mesure de la densité d’information binaire dans un mot donné.

Définition: Distance de Hamming (Hamming distance): La distance de Hamming entre deux mots de code de même longueur est le nombre de positions où ces deux mots diffèrent. Elle est notée $d_H(\cdot, \cdot)$ . Cette distance peut être calculée comme le poids de Hamming du XOR $\oplus$ des deux mots :
$d_H(\texttt{1100111, 0101101}) = w_H(\texttt{1100111} \oplus \texttt{0101101}) = w_H(\texttt{1001010}) = 3$
(3)

Définition: Distance minimale de Hamming: La distance minimale d’un code, notée $d_{\min}$ , est la plus petite distance de Hamming observée entre toutes les paires de mots de code valides du code considéré. Elle est un paramètre clé qui permet de déterminer la capacité du code à détecter ou corriger les erreurs :
$d_{\min} = \min_{i \ne j} d_H(\bm{c}_i, \bm{c}_j)$
(4)

Plus $d_{\min}$ est grand, plus le code est capable de détecter et corriger un plus grand nombre d’erreurs.

Codes Blocs¶

En utilisant les définitions précédentes, nous sommes maintenant prêts à définir les codes blocs. Un code bloc est une méthode de codage où des blocs fixes de $k$ bits d’information sont encodés en blocs de n bits appelés mots de code, où $n > k$ . Les paramètres fondamentaux d’un code bloc sont :

Dimension du code : $(n, k)$ , où $k$ est le nombre de bits d’information et $n$ le nombre total de bits dans le mot de code.
Taux de code :
$R = \frac{k}{n}$
(5)
qui indique l’efficacité du code en termes de bits d’information transmis.
Distance minimale : $d_{\min}$ , la plus petite distance de Hamming entre deux mots de code distincts. Elle détermine la capacité de détection et de correction d’erreurs.
Redondance :
$m = n - k$
(6)
le nombre de bits ajoutés pour assurer la protection contre les erreurs.

Codage¶

Dans un code bloc, un vecteur d’information $\bm{d} = [d_1, d_2, \ldots , d_k]$ est encodé en un mot de code $\bm{c} = [c_1, c_2, \ldots , c_n]$ , où $n > k$ . Le processus d’encodage introduit des bits de parité $[c_{k+1}, \ldots , c_n]$ qui sont calcu lés à partir des bits d’information. Ces bits de parité assurent la détection et la correction des erreurs, et ces bits sont calculés à l’aide de la matrice de génération. Pour les codes systématiques la matrice $\bm{G}$ combine une matrice identité $\bm{I_k}$ et une matrice $\bm{P}$ définissant les relations de parité,

\bm{G}= [\bm{I_k} \ | \ \bm{P}]

(7)

Les bits de parité $c_{k+1}, \ldots , c_n$ sont obtenus à partir des bits d’information $d_1, , d_k$ à l’aide des équations de parité (relations linéaires) suivantes

\begin{align*} c_{k+1} &= h_{1,1} d_1 \oplus h_{1,2} d_2 \oplus \ldots \oplus h_{1,k} d_k, \\ c_{k+2} &= h_{2,1}d_1 \oplus h_{2,2}d_2 \oplus \ldots \oplus h_{2,k}d_k, \\ &\\ c_n &= h_{m,1}d_1\oplus h_{m,2}d_2 \oplus \ldots \oplus h_{m,k}d_k, \end{align*}

(8)

où $\bm{P} = [h_{i,j}]$ est une matrice $k\times m$ définissant les relations de parité. Donc codeage est possible en utilisant

\bm{c} = \bm{d} \bm{G}

(9)

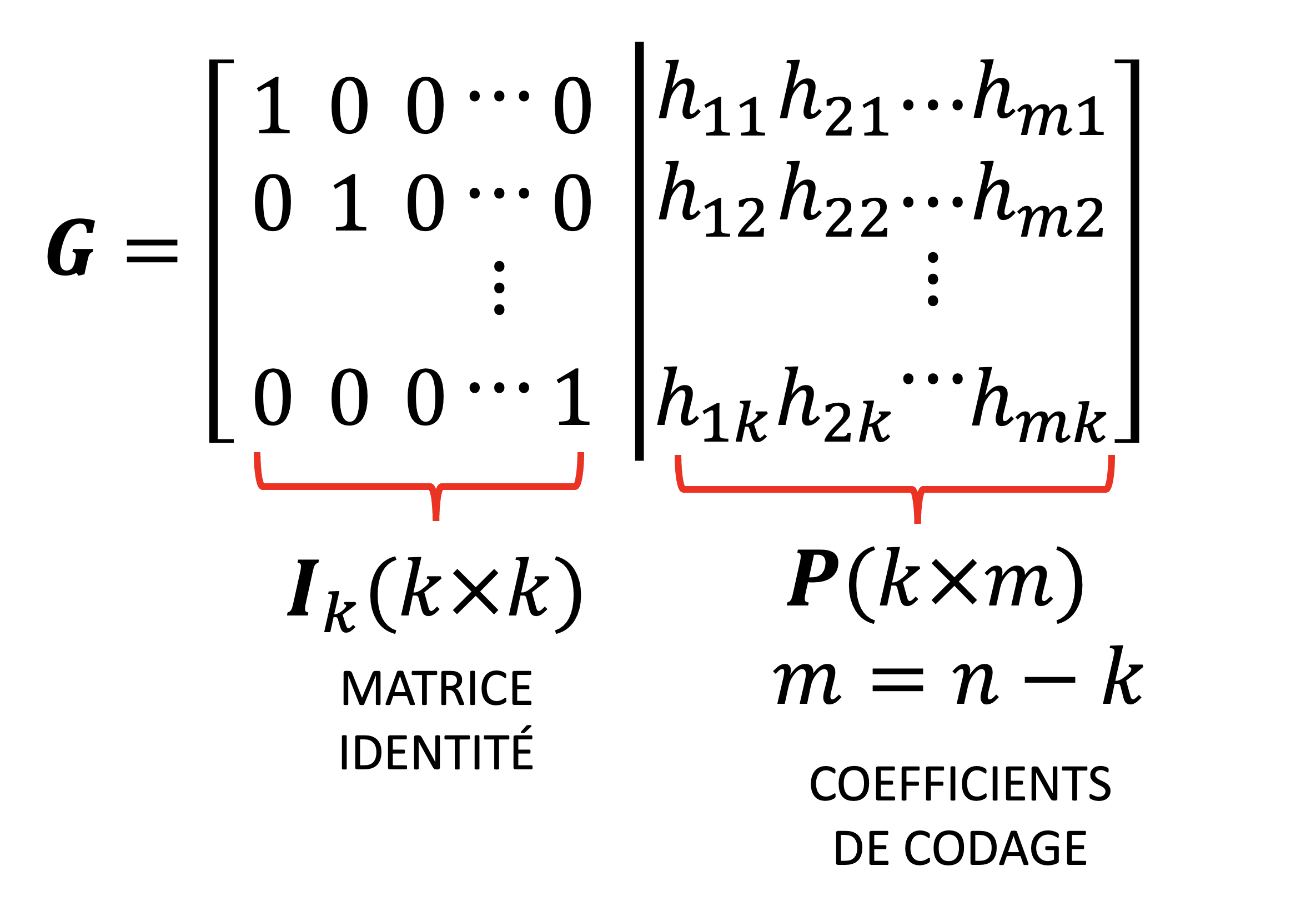
Structure d’une matrice de génération systématique \bm{G} : la matrice \bm{G} d’un code linéaire systématique est composée de deux parties : une matrice identité \bm{I}_k de taille k \times k à gauche, et une matrice de redondance \bm{P} de taille k \times m à droite, où m = n - k . Cette structure permet de conserver les bits d’information inchangés dans le mot de code tout en y ajoutant des bits de redondance calculés à l’aide de \bm{P} . — Figure 2:Structure d’une matrice de génération systématique $\bm{G}$ : la matrice $\bm{G}$ d’un code linéaire systématique est composée de deux parties : une matrice identité $\bm{I}_k$ de taille $k \times k$ à gauche, et une matrice de redondance $\bm{P}$ de taille $k \times m$ à droite, où $m = n - k$ . Cette structure permet de conserver les bits d’information inchangés dans le mot de code tout en y ajoutant des bits de redondance calculés à l’aide de $\bm{P}$ .

Codage linéaire d’un mot de code : Le vecteur d’information \bm{d} = [d_1, d_2, \ldots, d_k] est transformé en un mot de code \bm{c} = [c_1, c_2, \ldots, c_n] à l’aide d’un codeur de canal linéaire défini par une matrice de génération \bm{G} , selon la relation \bm{c} = \bm{d} \bm{G} . — Figure 3:Codage linéaire d’un mot de code : Le vecteur d’information $\bm{d} = [d_1, d_2, \ldots, d_k]$ est transformé en un mot de code $\bm{c} = [c_1, c_2, \ldots, c_n]$ à l’aide d’un codeur de canal linéaire défini par une matrice de génération $\bm{G}$ , selon la relation $\bm{c} = \bm{d} \bm{G}$ .

Pouvoirs détecteur et correcteur d’un code¶

Un code peut être utilisé soit pour détecter, soit pour corriger les erreurs.

Un code a un pouvoir détecteur de $t$ s’il peut assurer la détection de toute combinaison de $t$ erreurs ou moins dans un mot de code. Cela signifie qu’aucune de ces erreurs ne peut passer inaperçue. Le pouvoir détecteur est directement relié à la distance minimale $d_{\min}$ du code :
$t = d_{\min} - 1$
(10)
Un code a un pouvoir correcteur de $t$ s’il peut corriger toute combinaison de $t$ erreurs ou moins dans un mot de code. Cela signifie que même si des bits sont corrompus, le récepteur peut reconstruire le mot original. Le pouvoir correcteur dépend également de $d_{\min}$ , selon la parité de cette valeur :
$t = \left\{ \begin{array}{ll} \dfrac{d_{\min} - 1}{2} & \text{si } d_{\min} \text{ est impair} \\ \\[-0.8em] \dfrac{d_{\min}}{2} - 1 & \text{si } d_{\min} \text{ est pair} \end{array} \right.$
(11)

Ces formules sont essentielles pour concevoir des codes capables de détecter ou corriger un certain nombre d’erreurs, en fonction de la robustesse requise du système de communication.

Décodage¶

Nous savons que le canal peut ajouter un vecteur d’erreur au mot de code. On définit le vecteur d’erreur (mot d’erreur) comme

\bm{e} = [e_1, e_2, \dots, e_n]

(12)

où $e_i = \texttt{1}$ si le $i^\text{e}$ bit a été corrompu, et $e_i =\texttt{0}$ sinon.

Le mot reçu est la somme (modulo 2) du mot de code et de l’erreur :

\bm{r} = [r_1, r_2, \dots, r_n] = \bm{c} + \bm{e}

(13)

La correction d’erreurs repose sur le calcul d’un syndrome à partir du mot reçu et de la matrice de vérification. On calcule le syndrome

\bm{s} = [s_1, s_2, \dots, s_m] = \bm{r} \bm{H}^T

(14)

où $\bm{H}$ est la a matrice de vérification de parité (utilisée pour vérifier les mots de code reçus et détecter les erreurs).

Dans la forme générale :

\bm{H}= [\bm{P}^T \ | \ \bm{I}_m ]

(15)

où $\bm{P}^T$ est la transposée de $\bm{P}$ . Notez que

\bm{s} = \bm{r} \bm{H}^T = (\bm{c} + \bm{e}) \bm{H}^T = \bm{c} \bm{H}^T + \bm{e} \bm{H}^T

(16)

Mais $\bm{c} \bm{H}^T = \bm{0}$ pour tout mot valide (car $\bm{c} \in \text{Ker}(\bm{H}^T)$ ), on a :

\bm{s} = \bm{e} \bm{H}^T

(17)

En utilisant le syndrome, nous pouvons détecter et corriger les erreurs .

Exemple illustratif : Parité transversale, code(4,3)

Ce code est utiliser pour détecter un seul erreur, i.e. pour la vérification de parité. La matrice de génération associée est :

\bm{G} = \begin{bmatrix} \texttt{1} & \texttt{0} & \texttt{0} & \texttt{1} \\ \texttt{0} & \texttt{1} & \texttt{0} & \texttt{1} \\ \texttt{0} & \texttt{0} & \texttt{1} & \texttt{1} \\ \end{bmatrix}

(18)

La distance minimale de ce code est :

d_{\min} = 2

(19)

ce qui signifie qu’il est capable de détecter au plus :

t = d_{\min} - 1 = 1 \quad \text{erreur}

(20)

Le mot d’information à transmettre est un vecteur $\bm{d} = [d_1, d_2, d_3]$ . Ce vecteur est encodé en un mot de code $\bm{c} = [c_1, c_2, c_3, c_4]$ , où les trois premiers bits correspondent aux données et le dernier bit est un bit de parité défini comme :

c_4 = d_1 \oplus d_2 \oplus d_3

(21)

Supposons que l’information à transmettre soit $\bm{d} = [\texttt{110}]$ . Le mot de code correspondant est alors $\bm{c} = [\texttt{1100}]$ , car le bit de parité vaut $\texttt{1} \oplus \texttt{1} \oplus \texttt{0 = 0}$ . Si, au cours de la transmission, une erreur affecte le dernier bit (bit de parité), on reçoit le mot $\bm{r} = [\texttt{1110}]$ . En recalculant la parité sur les 4 bits reçus, on constate une incohérence : la parité est incorrecte. L’erreur est donc détectée.
Si deux erreurs surviennent (par exemple dans les bits 1 et 3), la parité recalculée peut coïncider avec la parité attendue, et l’erreur ne sera pas détectée. Cela montre une limitation du code.

Donc, ce code permet de détecter une seule erreur par mot de code, mais ne peut pas garantir la détection de deux erreurs.

Figure 4:Présentation du code code(4,3), parité transversale.

Exemple illustratif : Hamming systématique (7,4)

Les codes Hamming sont des codes blocs capables de détecter jusqu’à deux erreurs et de corriger une seule erreur. Considérons un code Hamming $(7, 4)$ avec les matrices suivantes :

\bm{G} = \begin{bmatrix} \texttt{1} & \texttt{0} & \texttt{0} & \texttt{0} & \texttt{1} & \texttt{1} & \texttt{0} \\ \texttt{0} & \texttt{1} & \texttt{0} & \texttt{0} & \texttt{1} & \texttt{0} & \texttt{1} \\ \texttt{0} & \texttt{0} & \texttt{1} & \texttt{0} & \texttt{0} & \texttt{1} & \texttt{1} \\ \texttt{0} & \texttt{0} & \texttt{0} & \texttt{1} & \texttt{1} & \texttt{1} & \texttt{1} \end{bmatrix},

(22)

\bm{H} = \begin{bmatrix} \texttt{1} & \texttt{1} & \texttt{0} & \texttt{1} & \texttt{1} & \texttt{0} & \texttt{0} \\ \texttt{1} & \texttt{0} & \texttt{1} & \texttt{1} & \texttt{0} & \texttt{1} & \texttt{0} \\ \texttt{0} & \texttt{1} & \texttt{1} & \texttt{1} & \texttt{0} & \texttt{0} & \texttt{1} \end{bmatrix}.

(23)

Encodage : Pour un vecteur d’information $\bm{d} = [\texttt{1 0 1 1}]$ , le mot de code est :
$\begin{align*} \bm{c} &= \bm{dG} = [\texttt{1 0 1 1 0 1 0}]. \end{align*}$
(24)
Décodage : Si le mot reçu est $\bm{r} = [\texttt{1 0 1 1 1 1 0}]$ , le syndrome est calculé comme :
$\begin{align*} \bm{s}&= \bm{rH}^T = [\texttt{1 0 0}]. \end{align*}$
(25)
Notez qu’il s’agit simplement de la troisième colonne de $\bm{H}$ . Ce syndrome indique une erreur au troisième bit . Après correction, le mot de code devient :
$\begin{align*} \bm{c} &= [\texttt{1 0 1 1 0 1 0}]. \end{align*}$
(26)

$Liste complète des mots de code. Ce code possède une distance minimale d_{\min} = 3 , ce qui signifie qu’il peut corriger jusqu’à une erreur t = \left\lfloor \frac{3 - 1}{2} \right\rfloor = 1 .$

Figure 5:Liste complète des mots de code. Ce code possède une distance minimale $d_{\min} = 3$ , ce qui signifie qu’il peut corriger jusqu’à une erreur $t = \left\lfloor \frac{3 - 1}{2} \right\rfloor = 1$ .

$Tableau de syndrome. Chaque ligne correspond à une erreur unique affectant l’un des 7 bits d’un mot de code. Ce tableau permet d’associer un syndrome unique à chaque bit erroné, ce qui rend possible la correction d’une erreur unique. Notez que chaque erreur correspond à une colonne de la matrice \bm{H}.$

Figure 6:Tableau de syndrome. Chaque ligne correspond à une erreur unique affectant l’un des 7 bits d’un mot de code. Ce tableau permet d’associer un syndrome unique à chaque bit erroné, ce qui rend possible la correction d’une erreur unique. Notez que chaque erreur correspond à une colonne de la matrice $\bm{H}$ .

Synthèse des étapes¶

La correction d’erreurs à l’aide d’un code linéaire se déroule en deux grandes phases : la construction du tableau des syndromes, puis la correction proprement dite d’un mot reçu. Ces étapes sont essentielles pour identifier puis corriger les erreurs survenues lors de la transmission.

Construction du tableau des syndromes: dans un premier temps, il est nécessaire de déterminer la distance minimale du code, notée $d_{\min}$ , ainsi que sa capacité de correction $t = \left\lfloor \frac{d_{\min} - 1}{2} \right\rfloor$ . Ensuite, on génère l’ensemble des schémas d’erreurs possibles, c’est-à-dire les vecteurs d’erreur contenant jusqu’à $t$ erreurs (au plus $t$ bits à 1). Ces vecteurs sont ceux que le code est capable de corriger. Pour chacun de ces vecteurs $\bm{e}$ , on calcule le syndrome associé $\bm{s} = \bm{e} \bm{H}^T$ , ce qui permet de construire un tableau qui associe chaque syndrome à une erreur probable. Ce tableau est utilisé comme référence lors de la réception. Si le code est systématique, le tableau des synromes correspond directement aux colonnes de $\bm{H}$
Correction des erreurs: Une fois le tableau de syndromes établi, la correction d’un mot reçu peut commencer. Lorsqu’un mot codé $\bm{r}$ est reçu, on commence par calculer son syndrome $\bm{s} = \bm{r} \bm{H}^T$ . Ce syndrome permet d’identifier le vecteur d’erreur $\bm{e}$ correspondant dans le tableau préalablement construit. Une fois $\bm{e}$ identifié, on corrige le mot reçu en calculant une estimation du mot de code original : $\hat{\bm{c}} = \bm{r} \oplus \bm{e}$ . Enfin, en connaissant la forme systématique du code (où les bits d’information sont inclus directement dans $\bm{c}$ ), on peut extraire le vecteur d’information estimé $\hat{\bm{d}}$ à partir de $\hat{\bm{c}}$ .

Conception de codes correcteurs¶

La conception de codes correcteurs d’erreurs est un processus complexe qui vise à répondre à des exigences spécifiques en matière de performance et de complexité. Elle commence par le choix des paramètres fondamentaux tels que la taille des blocs $(n, k)$ pour les codes blocs, ou la contrainte de longueur pour les codes convolutionnels.

Les critères de performance incluent la maximisation du taux de code $R = \frac{k}{n}$ , tout en assurant une redondance suffisante pour détecter et corriger efficacement les erreurs. Le type de code choisi dépend également de l’application visée : par exemple, les codes de Hamming sont souvent utilisés pour le stockage de données, tandis que les codes convolutionnels sont mieux adaptés aux transmissions continues comme dans les communications sans fil.

On distingue ainsi les codes blocs, qui encodent des blocs fixes de bits, des codes convolutionnels, qui produisent une séquence codée continue à l’aide de registres à décalage. Ces deux types de codes diffèrent également par leur complexité de décodage : les codes blocs utilisent des méthodes comme la détection par syndrome, souvent simples à mettre en œuvre, tandis que les codes convolutionnels requièrent des algorithmes plus complexes tels que Viterbi (cofondateur de Qualcom).

La stratégie de conception d’un code bloc comprend l’identification des contraintes du système, le choix des paramètres $(n, k)$ , la construction d’une matrice de génération $\bm{G}$ , ainsi que d’une matrice de vérification de parité $\bm{H}$ .

Toutefois, bien que ces principes soient introduits dans le cadre du cours afin de fournir une compréhension de base, le design avancé des codes — incluant l’optimisation algorithmique, la recherche de codes à distance minimale maximale ou encore l’analyse détaillée de la complexité de décodage — va au-delà du cadre de l’ELE3701.

Resumé¶

Section 6 introduit les principes du codage pour le contrôle des erreurs, une composante essentielle des systèmes de communication numériques modernes. Elle traite de O6. Utilisation des techniques de contrôle des erreurs pour garantir la fiabilité des transmissions et présente les motivations du codage de canal, qui vise à assurer l’intégrité des données transmises malgré les perturbations du canal (comme le bruit thermique ou les interférences). Deux grandes familles de codes sont détaillées : les codes blocs et les codes convolutionnels. La section explique comment les bits d’information sont transformés en mots de code par un codeur, en ajoutant de la redondance utile à la détection et à la correction d’erreurs. Sont également abordés les concepts clés tels que le poids et la distance de Hamming, la construction des matrices de génération et de vérification, ainsi que l’utilisation du syndrome pour identifier les erreurs. Enfin, la stratégie de conception d’un code est brièvement exposée, tout en soulignant que le design approfondi de codes dépasse le cadre du cours. L’objectif final est d’outiller l’étudiant pour analyser la fiabilité d’un lien de communication et comprendre le rôle des techniques de codage dans l’amélioration des performances du système.

Introduction

Exemples Intréractifs: Canaux de Transmission

Introduction

Exemples Intéractifs: Contrôle des erreurs