Abstract¶
Section 4 présente les principales techniques de modulation essentielles pour l’adaptation des signaux aux caractéristiques du canal de transmission. Elle commence par la modulation d’amplitude, qui consiste à faire varier l’amplitude de l’onde porteuse en fonction du signal modulant, incluant des variantes telles que la modulation à double bande latérale (DSB), la modulation à bande latérale unique (SSB) et la modulation d’amplitude en quadrature (QAM). Ensuite, la section aborde la modulation d’angle, qui regroupe la modulation de fréquence (FM) et la modulation de phase (PM), deux techniques qui modifient respectivement la fréquence et la phase de la porteuse pour améliorer la robustesse aux interférences et aux distorsions. Enfin, la section explore les principes de la modulation numérique, où l’information est transmise sous forme de symboles discrets, englobant des schémas tels que ASK (Amplitude Shift Keying), PSK (Phase Shift Keying) et QAM numérique. L’objectif O4 est de proposer les techniques de modulation les plus adaptées en fonction des caractéristiques du canal et du type d’information à transmettre, en mettant en lumière leurs avantages et leurs contraintes dans divers contextes de communication.
Introduction¶
La modulation est une étape essentielle des procédures de transmission dans les systèmes de communication modernes. Elle permet d’adapter le signal aux caractéristiques du canal, d’améliorer la qualité de transmission et d’optimiser l’utilisation du spectre. Différents types de modulation sont utilisés en fonction des besoins et des contraintes spécifiques de la transmission, qu’elle soit analogique ou numérique.
- Définition: Modulation
- La modulation est une procédure de transmission qui consiste à superposer un signal d’information our une onde porteuse, , ou un train d’impulsions composé de , afin de permettre son acheminement à travers un canal de communication. Elle est indispensable pour configurer l’utilisation du spectre, réduire les interférences et adapter le signal aux caractéristiques du support de transmission.
- Définition: Signal de message
- Le signal de message, , représente l’information avant toute modification ou modulation. Il peut être analogique (continu dans le temps et en amplitude, comme la musique) ou numérique (discret en amplitude et en temps, comme des données binaires). Le signal est souvent en bande de base (i.e. ses composantes fréquentielles sont centrées autour de 0 Hz) avec une largeur de bande de Hz.
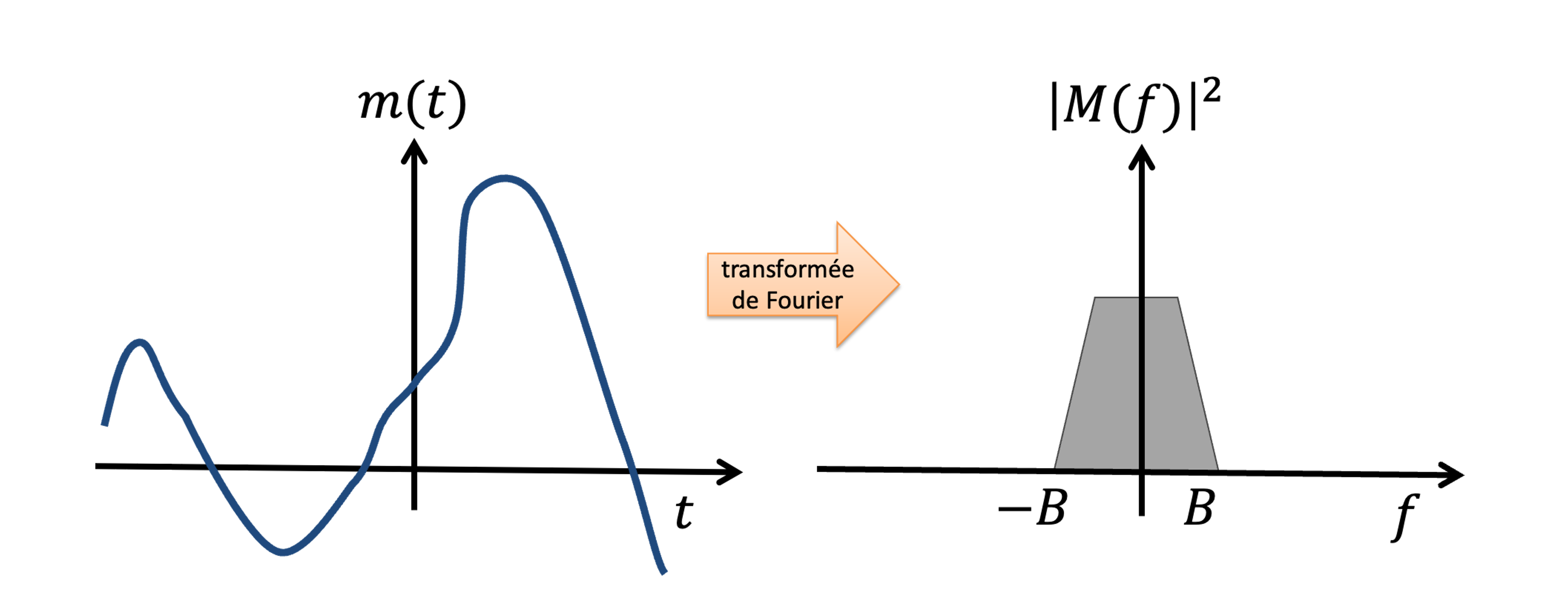
Figure 1:Un signal de message en bande de base avec une largeur de bande de Hz.
La modulation peut être réalisée en utilisant soit une onde porteuse, soit un train d’impulsions.
- Définition: Onde Porteuse
- Une onde porteuse (carrier waveform), (e.g. ), est un signal sinusoïdal de fréquence utilisé en modulation pour transporter un signal de message en modifiant son amplitude, sa fréquence ou sa phase. L’amplitude, la phase ou la fréquence de la forme d’onde porteuse est modifiée en fonction du signal du message, , avec une largeur de bande . La fréquence de la porteuse doit être choisie plus grande que la largeur de bande,
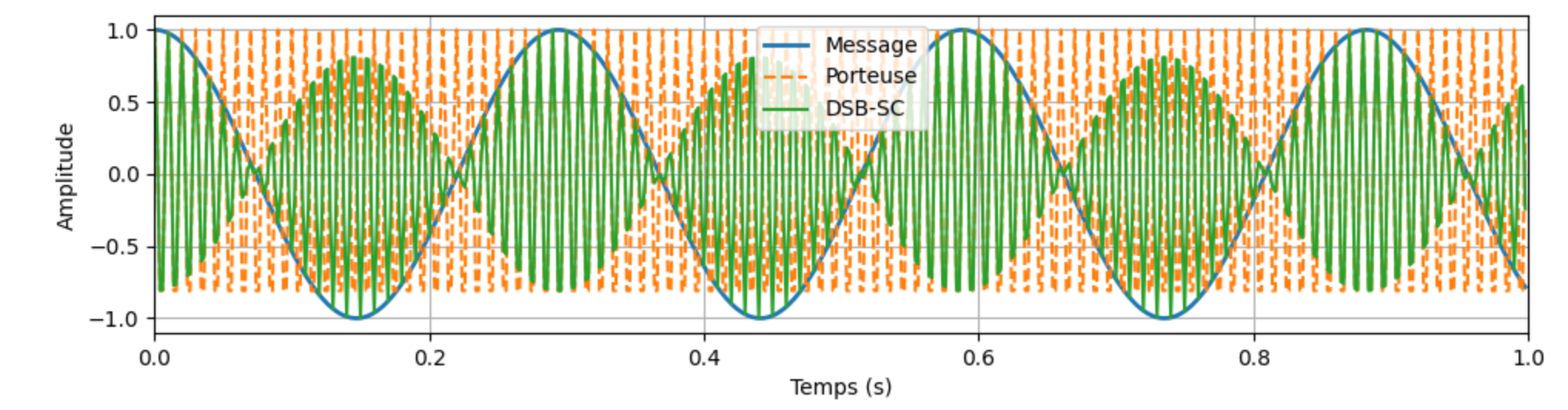
Figure 1:Un signal de message et l’onde porteuse. Le signal modulé est . (Voir: Exemples Intéractifs: Procédures de transmission - Modulation DSB-SC)
- Définition: Train d’impulsions
- Il est également possible de transmettre des signaux sans utiliser une porteuse haute fréquence. Dans ce cas, un train d’impulsions est nécessaire; Notez que la période du train d’impulsions est notée , et elle sera utilisée pour représenter la période du symbole.
Catégories de modulation¶
Les types de modulation peuvent être classés en fonction de la nature du signal de message. Si le signal de message est continu dans le temps et en amplitude, le système est appelé modulation analogique. En revanche, si le message discret en amplitude et en temps, il est qualifié de modulation numérique.
Les types de modulation peuvent également être classés en fonction de la présence d’une fréquence porteuse. La transmission en bande de base signifie que le signal est envoyé directement sans être transposé sur une fréquence porteuse. Cette technique est généralement utilisée pour les transmissions sur des distances courtes, comme les réseaux informatiques ou certaines applications industrielles. Contrairement à la bande de base, la transmission par onde porteuse repose sur une porteuse haute fréquence , ce qui permet d’envoyer les signaux sur de longues distances et d’optimiser l’utilisation du spectre.
Table 1:Catégories de modulation
| Catégories de modulation | Transmission en bande de base (avec train d’impulsion) | Transmission par onde porteuse |
|---|---|---|
| Analogique | Modulation d’amplitude : « PAM : Pulse Amplitude Modulation » Modulation de durée : « PWM : Pulse Width Modulation » Modulation de position : « PPM : Pulse Position Modulation » | Modulation linéaire (Modulation d’amplitude) : « AM : Amplitude Modulation » et ses variations Modulation d’angle : « PM : Phase Modulation » « FM : Frequency Modulation » |
| Numérique | Modulation par impulsions codées : « PCM : Pulse Code Modulation » Codage de ligne : « Line coding » | Modulations binaires : « FSK : Frequency Shift Keying » « BPSK : Binary Phase Shift Keying » Modulations multiniveaux (M) : « QPSK : Quadrature Phase Shift Keying » « M-FSK : Frequency Shift Keying » « M-QAM : M-ary Quadrature AM » « M-PSK : M-ary Phase Shift Keying » |
Critères de performance des techniques de modulation¶
Les deux critères de performance sont l’efficacité énergétique et l’efficacité spectrale.
- Définition: L’efficacité énergétique
- L’efficacité énergétique (energy efficiency) est l’énergie (puissance) du signal de message divisée par l’énergie (puissance) du signal modulé L’efficacité énergétique mesure de la capabilité d’un système à utiliser efficacement l’énergie pour transmettre des signaux de message.
- Définition: L’efficacité spectrale
- L’efficacité spectrale (spectral efficiency) mesure la quantité de signaux de message transmises par unité de largeur de bande. Pour les systèmes de modulation analogiques, elle est obtenue en divisant la largeur de bande du signal de message par la largeur de bande du signal modulé.
Pour les systèmes de modulation numérique, nous le définirons comme le nombre de bits transmis par Hertz [bits/sec/Hz], qui change en fonction du type d’image et du type de modulation sélectionnés (plus de détails à venir).
Catégories de modulation par onde porteuse¶
La modulation par onde porteuse peut affecter l’amplitude, la phase ou la fréquence d’une onde porteuse pour transmettre un signal de message, qu’il soit analogique ou numérique.
Le signal modulé, , par une onde porteuse est exprimée sous la forme
où représente l’amplitude du signal modulé, est la fréquence porteuse qui peut varier en temp, et correspond à la phase du signal modulé.
Ci-dessous se trouve une explication de certains types de modulation:
1. Modulation d’amplitude analogique (Amplitude modulation - analog)
- Le signal de message est analogique.
- L’amplitude de la porteuse varie en fonction de .
Types :
- Modulation à double bande latérale sans porteuse « DSB-SC : Double-sideband suppressed-carier »
- Modulation à double bande latérale « AM : Amplitude modulation »
- Bande latérale unique « SSB : Single sideband »
- Modulation d’amplitude en quadrature (analogique) « QAM : Quadrature amplitude modulation»
2. Modulation d’angle analogique (Angle modulation - analog) Ce type de modulation concerne la phase ou la fréquence de la porteuse :
- Le signal de message est analogique.
- La phase (ou la fréquence ) varie en fonction de .
Types :
- Modulation de phase « PM : Phase modulation »
- Modulation de fréquence « FM : Frequency modulation »
3. Modulation numérique Ce type de modulation s’applique aux signaux numériques :
- Le message est numérique (valeurs discrètes, binaires ou multiniveaux).
- L’amplitude et/ou la phase varient en fonction de .
Types :
- « ASK : Amplitude Shift Keying »
- « FSK : Frequency Shift Keying »
- « PSK : Phase Shift Keying »
- « QAM : Frequency Shift Keying »
Modulation d’amplitude (analogique)¶
Les types de modulation d’amplitude analogique peuvent être classés en fonction de la manière dont l’information est transmise à travers l’onde porteuse. La modulation à double bande latérale sans porteuse (Double-Sideband Suppressed-Carrier; DSB-SC) supprime la composante continue de l’onde porteuse pour améliorer l’efficacité énergétique et spectrale. La modulation à double bande latérale (Amplitude Modulation; AM), quant à elle, transmet l’information en modulant l’amplitude d’une onde porteuse et en ajoutant une petite partie de la porteuse tout en deux bandes latérales. La modulation à bande latérale unique (Single Sideband; SSB) optimise encore plus l’utilisation du spectre en supprimant l’une des deux bandes latérales, réduisant ainsi la largeur de bande requise. Enfin, la modulation d’amplitude en quadrature (Quadrature Amplitude Modulation; QAM) combine deux signaux modulés en amplitude, déphasés de 90°, permettant ainsi une transmission plus efficace de l’information analogique avec une meilleure utilisation du spectre. Les détails de ces types de modulations analogiques sont expliqués ci-dessous.
Modulation à double bande latérale porteuse supprimée (DSB-SC)¶
Modulation à double bande latérale porteuse supprimée (double sideband suppressed carrier; DSB-SC) implique la multiplication du signal du message, ( limité à une bande de fréquence de Hz), une porteuse (onde sinusoïdale) de fréquence , notée .
- Modulation
Le signal modulé est donné par :
Ce signal ne contient plus la porteuse mais uniquement les bandes latérales.
En transformée de Fourier, le spectre du signal modulé est :
Cela montre que le spectre du signal est déplacé autour de .
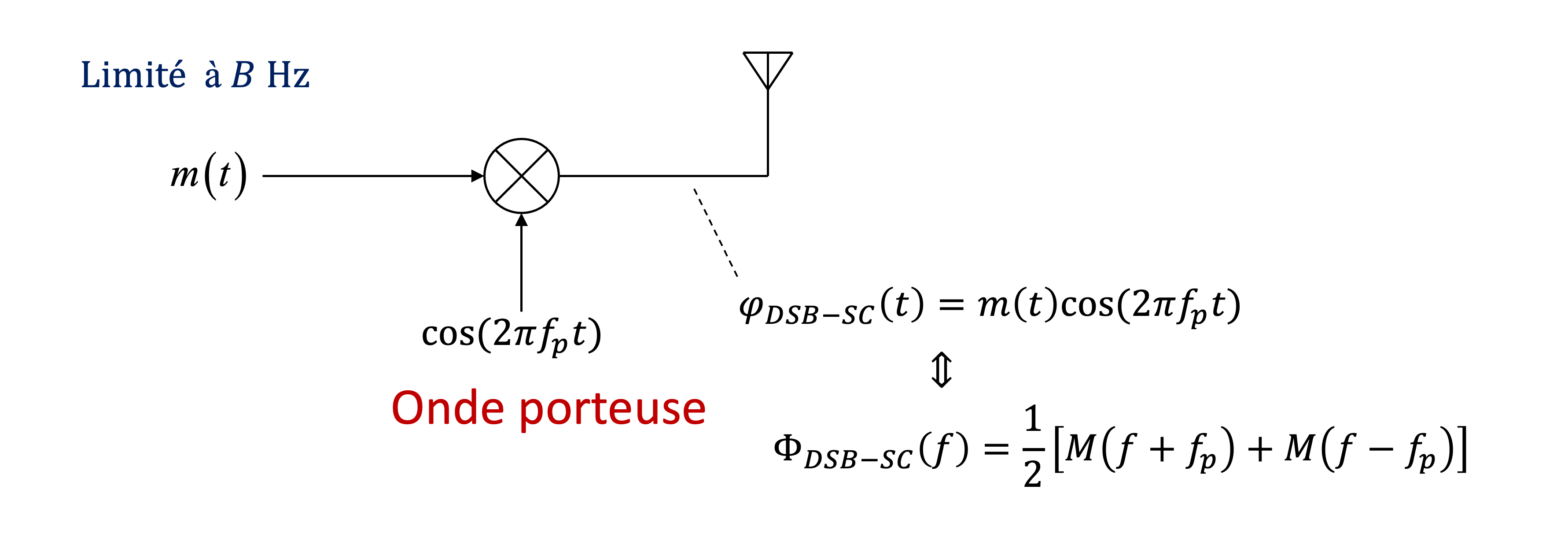
Figure 3:Schéma de la modulation DSB-SC, où le signal est multiplié par une porteuse , déplaçant ainsi son spectre autour de .
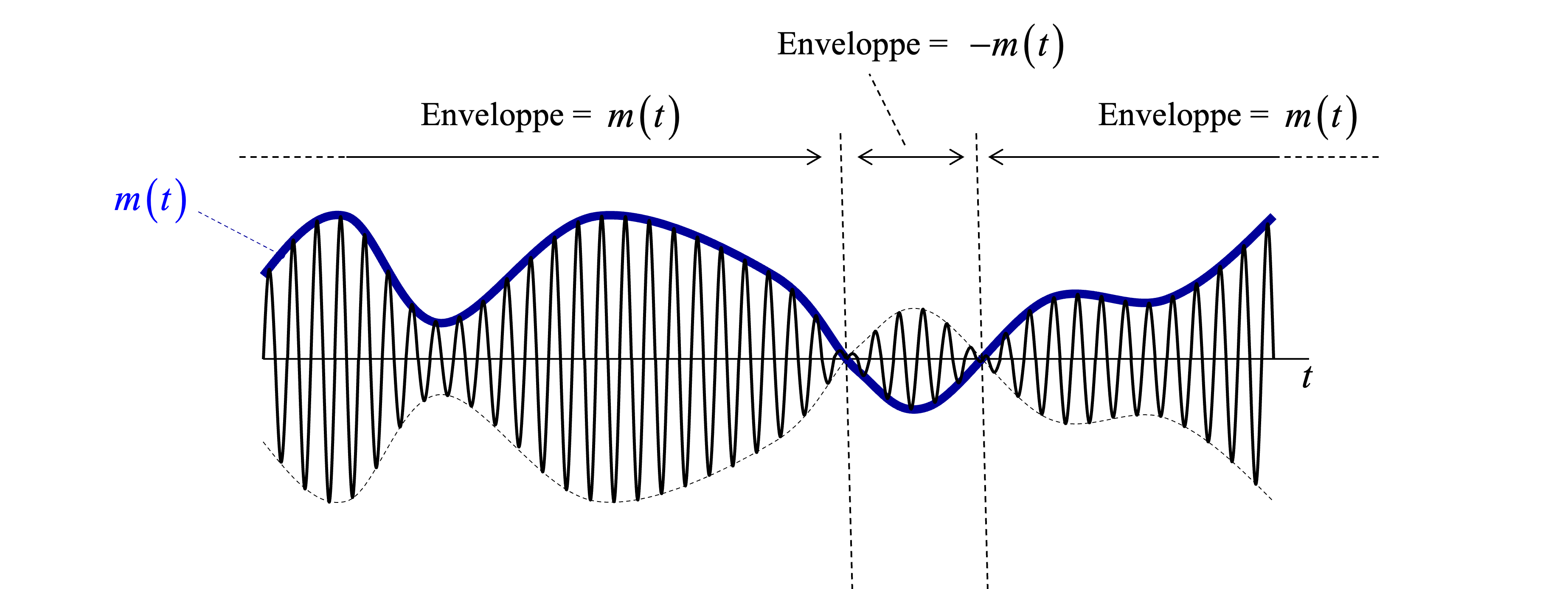
Figure 4:Une illustration de la modulation DSB-SC, où le signal module la porteuse , pour générer .
- Efficacité énergétique
L’efficacité énergétique est définie comme le rapport entre la puissance moyenne du signal message et celle du signal modulé . Dans le cas de la modulation DSB-SC, la puissance moyenne du signal modulé est :
Donc, l’efficacité énergétique de la modulation DSB-SC est :
Cela signifie que 50% de la puissance du signal modulé est contenue dans le signal message . La porteuse est supprimée (car il l y a pas une composante en ), ce qui améliore l’efficacité énergétique du signal transmis.
- Efficacité spectrale
Le spectre du signal modulé contient deux bandes latérales, ce qui double la largeur de bande du signal modulé par rapport au signal message,
Ainsi, l’efficacité spectrale de la modulation DSB-SC est :
Cela signifie que seulement 50% de la largeur de bande du signal modulé est effectivement utilisée pour transmettre l’information.
![L’image à gauche représente le spectre du signal de message m(t). L’image à droite représente le spectre du signal après modulation DSB-SC. Les deux bandes latérales sont identiques et contiennent chacune la moitié de la puissance du signal d’origine, car \Phi_{DSB-SC}(f) = \frac{1}{2} \left[ M(f + f_p) + M(f - f_p) \right].](/build/sec4-DSB-spectre-920ee7b0b024918cd49c60a6583d2efa.png)
Figure 5:L’image à gauche représente le spectre du signal de message . L’image à droite représente le spectre du signal après modulation DSB-SC. Les deux bandes latérales sont identiques et contiennent chacune la moitié de la puissance du signal d’origine, car .
- Démodulation cohérente (synchrone)
Le signal modulé reçu est filtré par un filtre passe-bande, qui réduit la puissance du bruit et ne laisse passer que les fréquences entre et .
Dans le cas idéal, Le filtre a une réponse en fréquence donnée par :
Le signal filtré est multiplié par une porteuse locale au récepteur :
La porteuse générée peut ne pas être parfaitement alignée avec celle de l’émetteur, ce qui introduit un décalage de phase (problème de synchronisation).
Après la multiplication avec la porteuse locale, le signal passe dans un filtre passe-bas avec une fréquence de coupure , et gain de 2, qui supprime les hautes fréquences et ne conserve que la composante basse fréquence du signal.
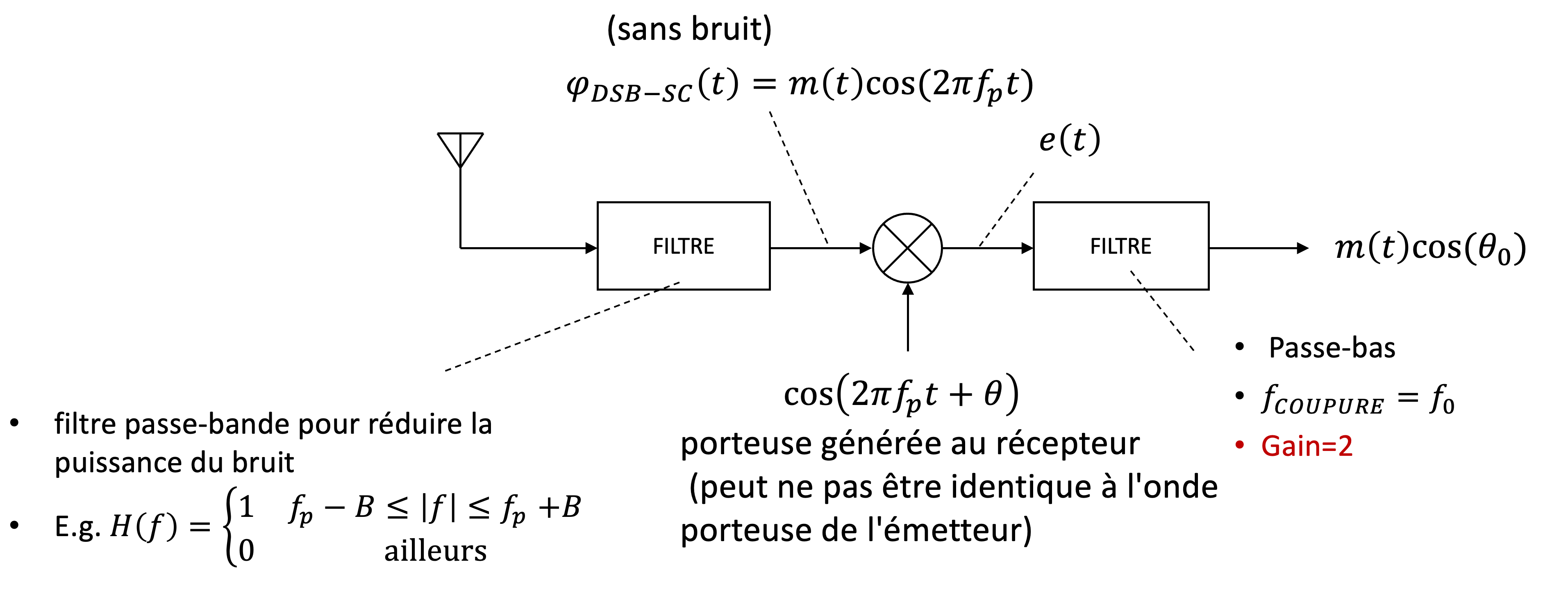
Figure 6:Schéma de la démodulation cohérente d’un signal DSB-SC. Un filtre passe-bande réduit le bruit avant la multiplication avec une porteuse locale. Un filtre passe-bas extrait ensuite le signal message, avec un effet de synchronisation dépendant du décalage de phase θ.
Modulation à double bande latérale (Amplitude modulation; AM)¶
- Modulation
Le signal de message et l’onde porteuse sont combinés pour former :
Le terme est un gain choisi pour garantir que , évitant ainsi toute inversion de phase (pour détecteur d’enveloppe).
Le spectre du signal modulé est :
Cela montre que le spectre du signal est déplacé autour de , et contient une composante en fréquence
- Définition: Indice de modulation (Modulation index)
- Indice de modulation, est défini par :
Il représente le rapport entre l’amplitude maximale du signal message et l’amplitude de la porteuse .
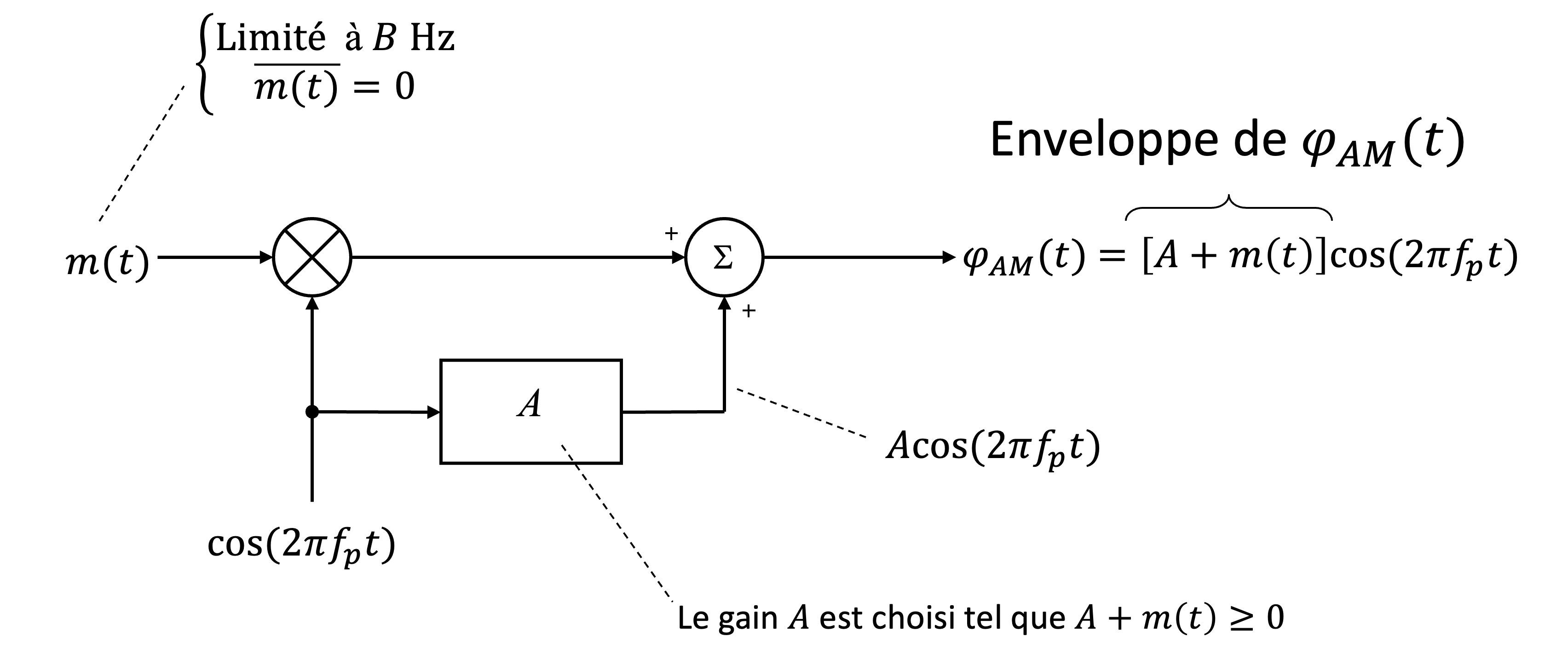
Figure 8:Schéma du processus de modulation d’amplitude (AM), où le signal de message module l’amplitude d’une porteuse , en ajoutant un terme constant pour éviter toute inversion de phase.
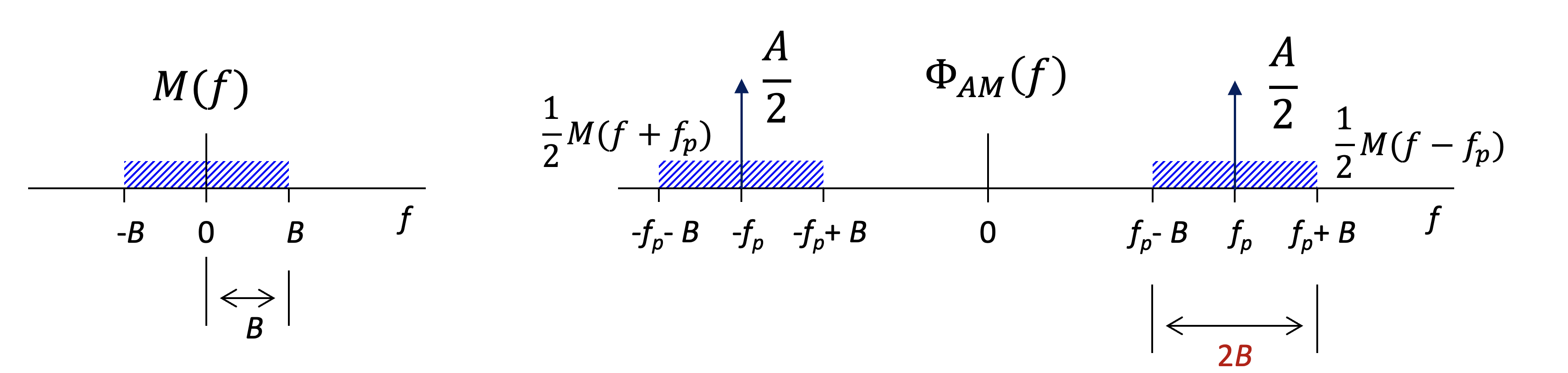
Figure 9:Représentation fréquentielle du signal AM. Le spectre du signal de message , initialement centré autour de 0 Hz, est déplacé autour de .
- Efficacité énergétique
L’efficacité énergétique est définie comme le rapport entre la puissance moyenne du signal message et celle du signal modulé .
D’après la puissance moyenne du signal AM donnée :
L’efficacité énergétique devient donc :
- Efficacité spectrale
L’efficacité spectrale du signal AM est :
- Démodulation non cohérente : Détecteur d’enveloppe (Envelope detector)
L’enveloppe d’un signal AM représente l’amplitude instantanée du signal modulé. Pour un signal AM donné par :
l’enveloppe est définie par :
Elle suit l’évolution du signal de message , assurant ainsi que l’information est préservée dans la modulation. Le détecteur d’enveloppe permet d’extraire cette enveloppe à partir du signal modulé. Il est généralement constitué de :
- Un redresseur (diode) qui élimine la partie négative du signal.
- Un circuit RC (résistance-capacité) qui agit comme un filtre passe-bas pour lisser les variations de la porteuse et récupérer l’enveloppe .
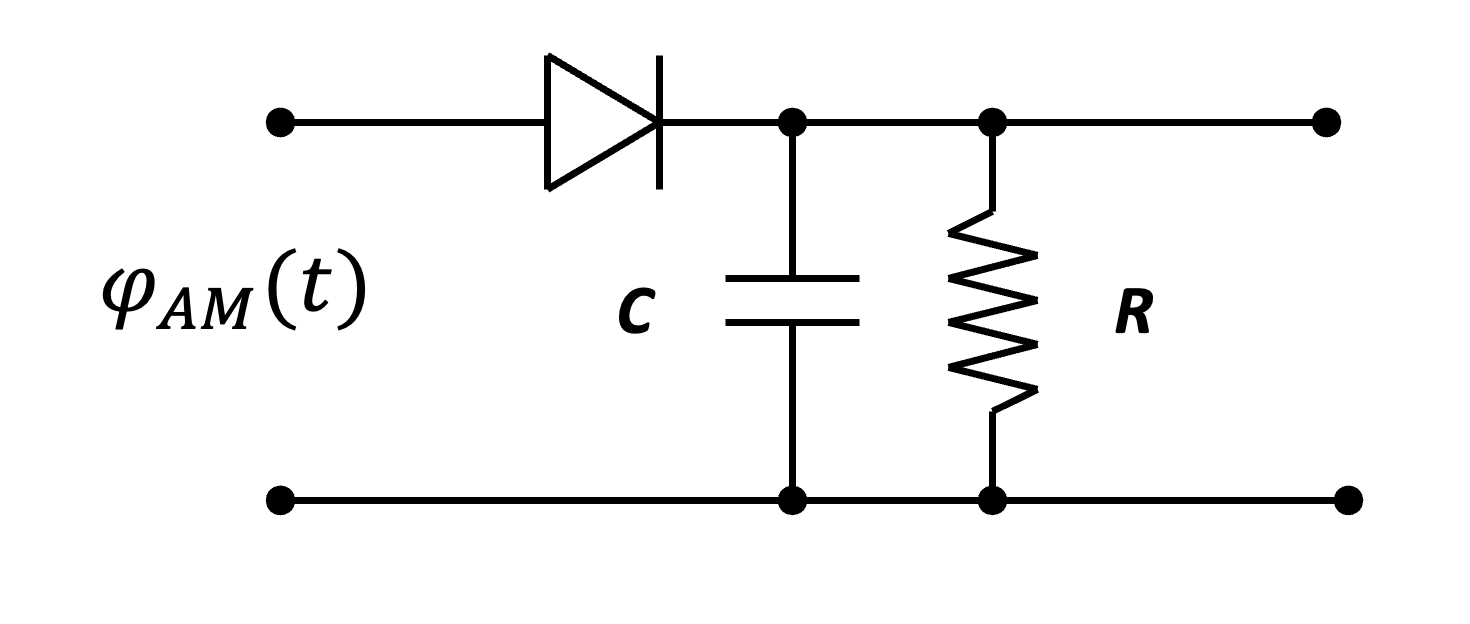
Figure 11:Schéma d’un détecteur d’enveloppe utilisé pour la démodulation AM. Le circuit est composé d’une diode pour redresser le signal, d’un condensateur CC pour stocker la charge et d’une résistance RR qui détermine la constante de temps RC, permettant de lisser l’enveloppe du signal modulé.
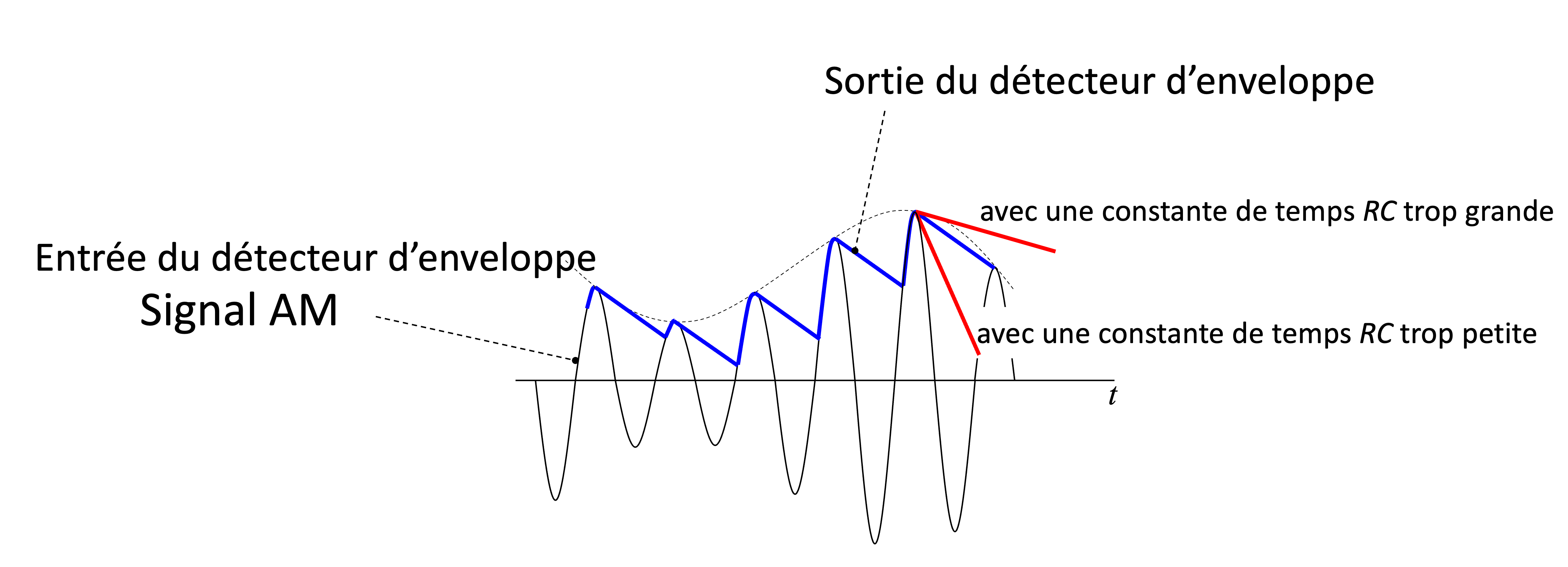
Figure 12:Illustration du fonctionnement du détecteur d’enveloppe pour un signal AM. L’entrée du détecteur est un signal AM (courbe noire). La courbe bleue représente une extraction correcte de l’enveloppe. Une mauvaise constante de temps RC peut soit ralentir la détection (courbe rouge supérieure) soit causer une distorsion (courbe rouge inférieure).
Pour que le détecteur d’enveloppe fonctionne correctement, deux conditions doivent être respectées :
Il faut que l’amplitude instantanée du signal modulé ne devienne jamais négative pour éviter toute inversion de phase. La condition mathématique est :
Cela impose que
La fréquence du signal message doit être beaucoup plus petite que la fréquence porteuse :
Cela garantit que l’enveloppe varie lentement par rapport aux oscillations rapides de la porteuse.
- Démodulation cohérente (synchrone)
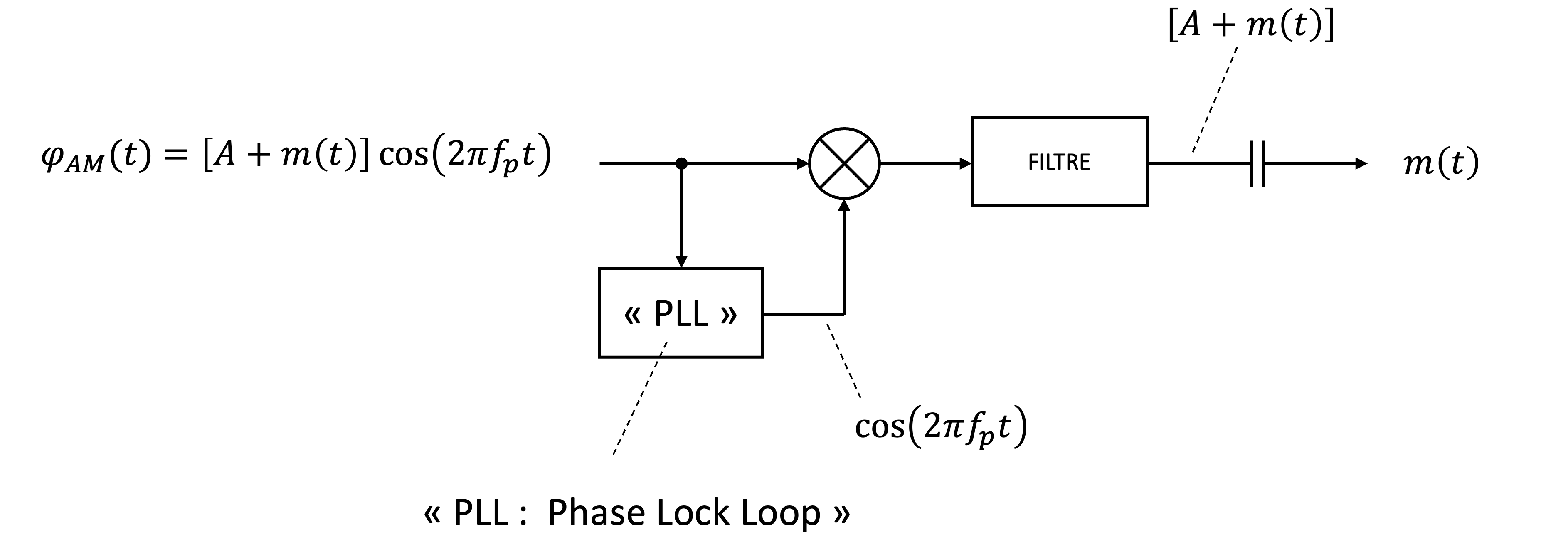
Figure 15:Schéma d’un démodulateur cohérente La figure illustre le principe de la démodulation cohérente d’un signal AM en utilisant une PLL (phase locked loop). Cette méthode permet de récupérer avec précision le signal de message à partir du signal modulé, en synchronisant une porteuse locale avec celle du signal reçu.
Le signal modulé en entrée est donné par . L’objectif est d’extraire uniquement en éliminant la porteuse. Pour cela, le signal entre d’abord dans un mélangeur (mixer), qui effectue une multiplication avec un signal de référence . Cette opération produit deux termes : une composante basse fréquence correspondant à l’enveloppe et une composante haute fréquence centrée autour de .
Pour isoler le signal utile, un filtre passe-bas est appliqué après le mélangeur. Ce filtre élimine les hautes fréquences et ne conserve que la composante basse fréquence, soit . Notez que, à ce stade, bien que l’information du message soit récupérée, une erreur de phase pourrait perturber la démodulation si la porteuse locale utilisée dans le mélangeur n’est pas parfaitement synchronisée avec celle du signal reçu.
C’est à ce niveau qu’intervient la PLL (Phase Lock Loop). Ce circuit ajuste dynamiquement la fréquence et la phase de la porteuse locale pour s’assurer qu’elle est en parfaite synchronisation avec la porteuse du signal reçu. En maintenant cet alignement, la PLL permet d’éviter les erreurs de phase qui pourraient altérer la restitution du signal de message.
Finalement, à la sortie du filtre, on obtient , qui peut être traité pour supprimer la constante , généralement via un filtre passe-haut. Cette dernière étape permet d’obtenir uniquement le signal , qui est la réplique exacte du signal de message initialement modulé à l’émission. Ainsi, grâce à cette méthode cohérente, la démodulation est réalisée avec une précision élevée, rendant cette approche particulièrement utile dans les communications nécessitant une forte immunité aux distorsions et aux interférences.
Modulations efficaces du point au vue de la largeur de bande sont la Modulation à bande latérale unique (single sideband; SSB) et la modulation d’amplitude en quadrature (analogique) (quadrature amplitude modulation - analog; QAM-Analogique). Elles sont décrites ci-dessous.
Modulation à bande latérale unique (SSB)¶
Dans une modulation AM classique, l’information transmise est redondante, car elle est contenue à la fois dans la bande latérale supérieure et la bande latérale inférieure. Il est donc possible d’envoyer le même message en utilisant seulement une des deux bandes, réduisant ainsi de moitié la largeur de bande nécessaire.
- Modulation
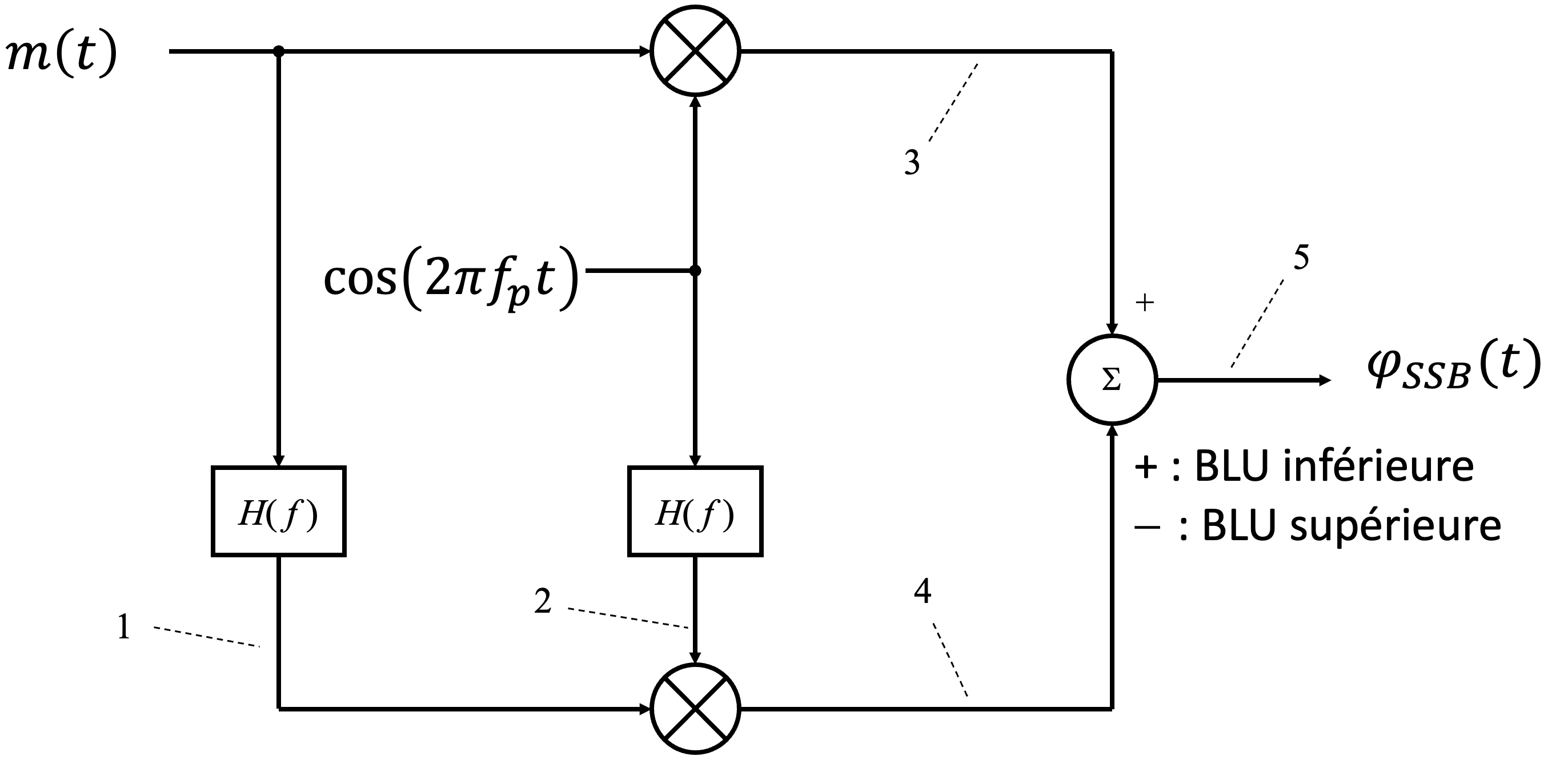
Figure 17:Illustration de la génération d’un signal SSB (Single Sideband) en utilisant la méthode par déphasage, qui permet de supprimer l’une des bandes latérales.
On utilise deux branches pour générer un signal modulé de SSB. Dans la première branche, est directement multiplié par la porteuse pour obtenir
Dans la deuxième branche, le signal est d’abord transformé par un filtre à déphasage , qui effectue un décalage de phase de (Transformée de Hilbert):
Ce signal est ensuite multiplié par une porteuse en quadrature :
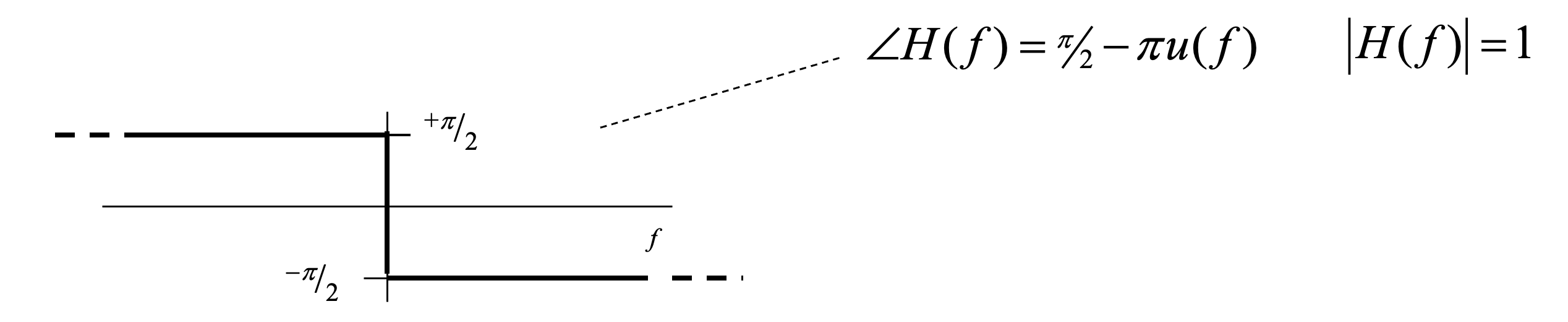
Figure 18:Représentation fréquentielle du filtre de Hilbert (déphasage) : la phase introduit un déphasage de pour les fréquences positives et de pour les fréquences négatives, tandis que le module reste constant à 1.
Finalement, les deux signaux obtenus sont combinés. Pour générer la bande latérale supérieure (upper sideband; USB), on effectue une addition :
Pour générer la bande latérale inférieure (lower sideband; LSB ), on effectue une soustraction :
L’expression en fréquence du signal SSB est obtenue en utilisant la transformée de Fourier :
- Pour la USB, le spectre est :
- Pour la BLI, le spectre est :
Grâce à cette approche, seule une des bandes latérales est transmise, ce qui permet de réduire de moitié la largeur de bande par rapport à une modulation AM conventionnelle. Cette technique est particulièrement utilisée dans les communications à bande limitée, comme la radio HF et certains systèmes de télécommunications analogiques avancés.
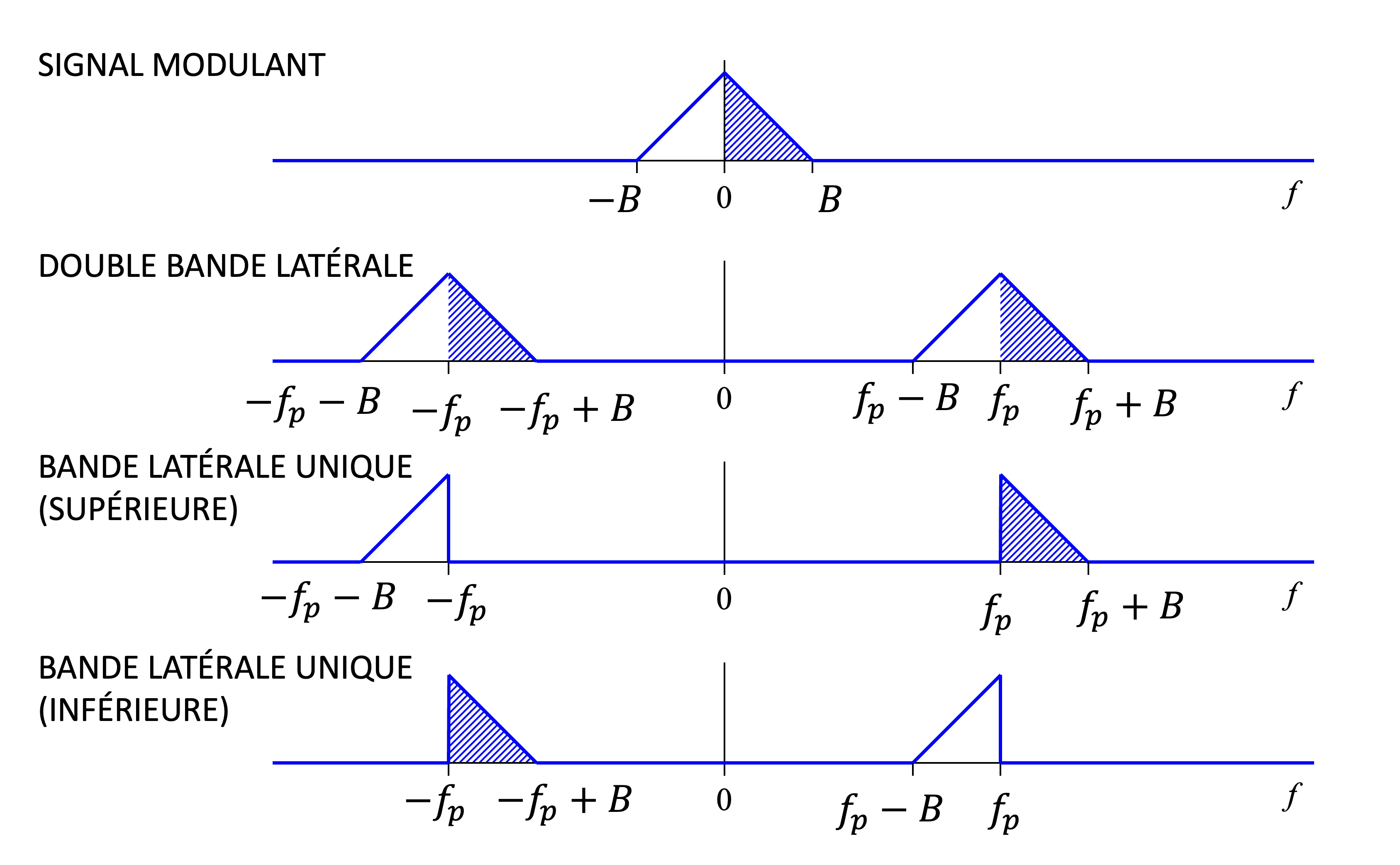
Figure 19:Représentation spectrale des différentes techniques de modulation en amplitude : (1) Signal modulant en bande de base, (2) Modulation à double bande latérale (DSB), (3) Modulation à bande latérale unique supérieure (SSB-USB), et (4) Modulation à bande latérale unique inférieure (SSB-LSB). La modulation SSB permet de réduire la largeur de bande nécessaire en ne transmettant qu’une seule bande latérale du spectre du signal modulé.
- Efficacité énergétique
Pour SSB (modulation à bande latérale unique) efficacité énergétique est
Efficacité spectrale
La largeur de bande occupée est ( B ), donc :Démodulation cohérente (synchrone)
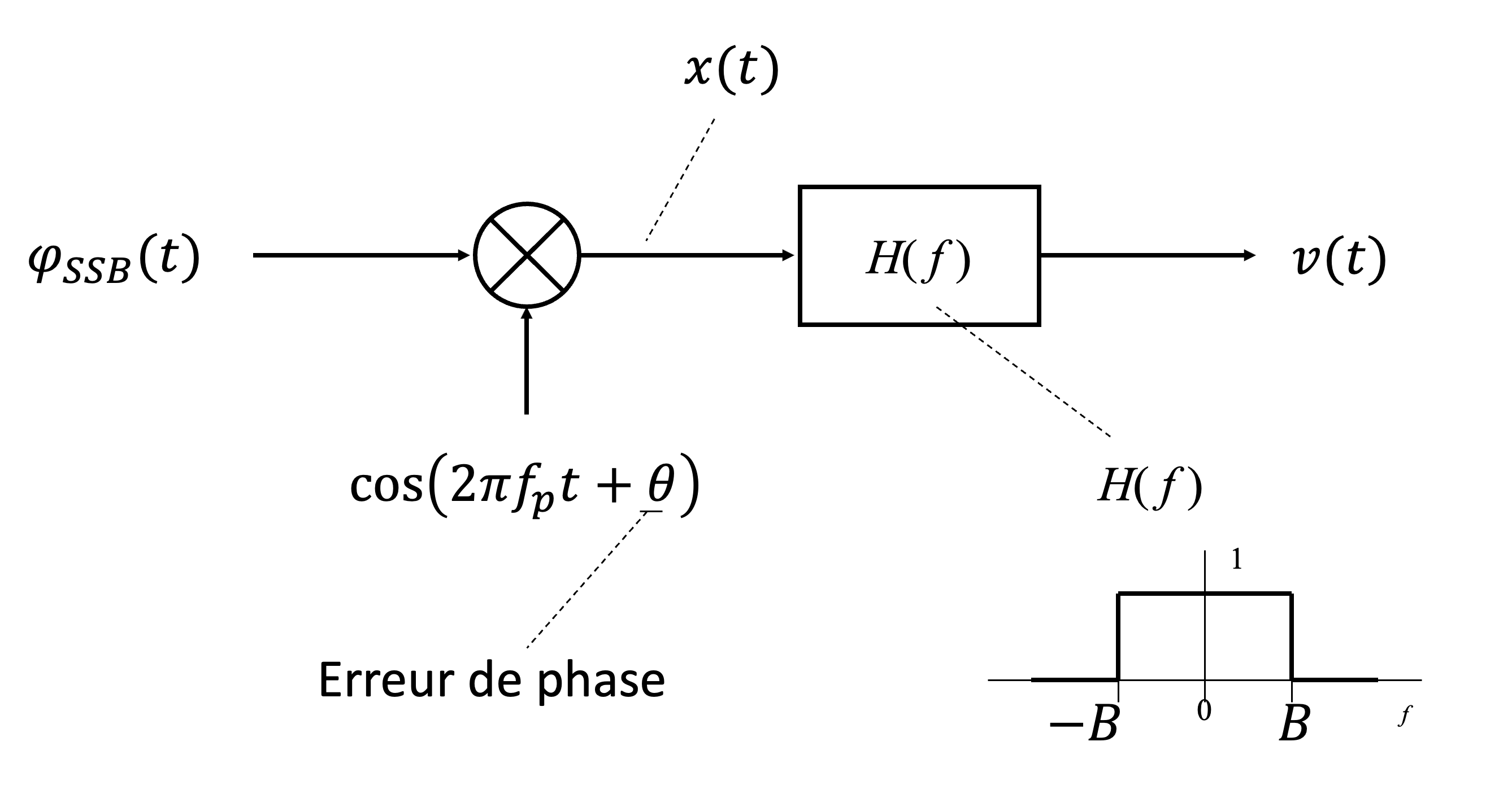
Figure 20:Démodulation d’un signal à bande latérale unique avec une erreur de phase dans l’oscillateur local. Un filtre passe-bas est utilisé pour récupérer le signal modulant, mais une erreur de phase peut causer une distorsion du signal démodulé.
Signal d’entrée est est le signal modulé en bande latérale unique qui arrive au récepteur. Il est multiplié par une porteuse locale , où θ représente une erreur de phase potentielle
Le signal obtenu après multiplication (mixing) est noté , et il peut contenir des composantes en bande de base ainsi que du bruit. Un filtre passe-bas est appliqué pour éliminer les composantes haute fréquence indésirables, conservant uniquement le signal souhaité,
Finalement, est le signal démodulé en bande de base, qui peut être affecté par l’erreur de phase , entraînant une distorsion du message.
Modulation d’amplitude en quadrature (analogique) (QAM-Analogique)¶
La modulation d’amplitude en quadrature (QAM-Analogique), permet la transmission simultanée de deux signaux distincts et en utilisant une onde porteuses avec deux phases (inphase et quadrature).
- Modulation
Nous avons deux signaux messages distincts, et , chacun d’eux possède une largeur de bande de Hz. Dans le cas d’une modulation en quadrature (QAM), ces deux signaux peuvent être transmis simultanément en les associant à des porteuses orthogonales, comme un cosinus et un sinus à une fréquence porteuse . L’utilisation de deux signaux de largeur de bande permet d’augmenter l’utilisation du spectre tout en assurant une séparation correcte des informations transmises.
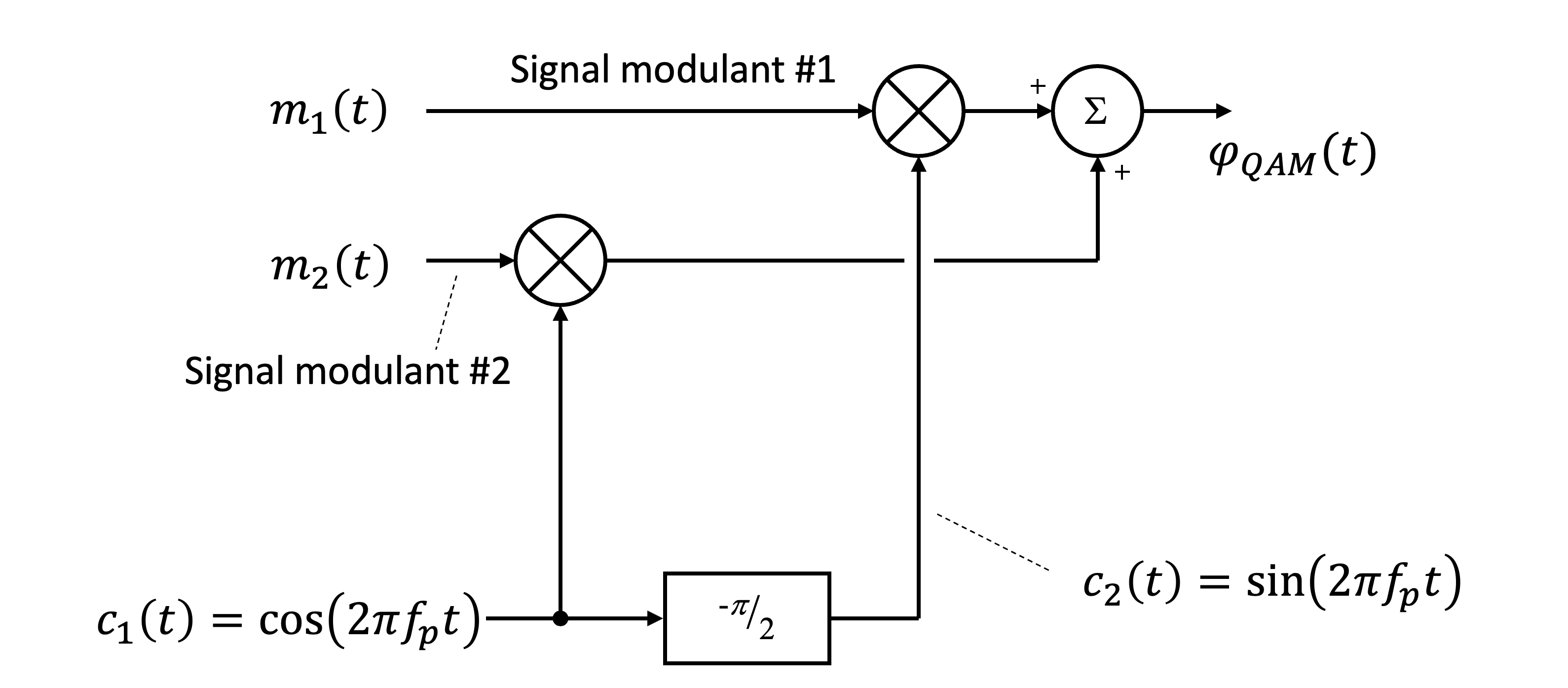
Figure 21:La modulation d’amplitude en quadrature (QAM-Analogique) permettant la transmission simultanée de deux signaux et grâce à l’utilisation de deux porteuses orthogonales en cosinus et en sinus avec .
Le signal module une porteuse en cosinus :
Le signal après le multiplexage est :
Dans la deuxième branche, le signal module une porteuse en sinus, obtenue par un déphasage de :
Le signal après le multiplexage avec est :
La somme des deux signaux forme le signal QAM-A :
- Efficacité énergétique
Dans le cas de la modulation QAM-A avec deux signaux et , l’efficacité énergétique est :
Supposons que les deux signaux et ont la même puissance,
- Efficacité spectrale
Pour la modulation QAM-A, la largeur de bande du signal modulé est égale à celle du message , car chaque signal et occupe la même bande de fréquence, et l’orthogonalité des porteuses permet d’éviter l’élargissement du spectre, donc
- Démodulation cohérente (synchrone)
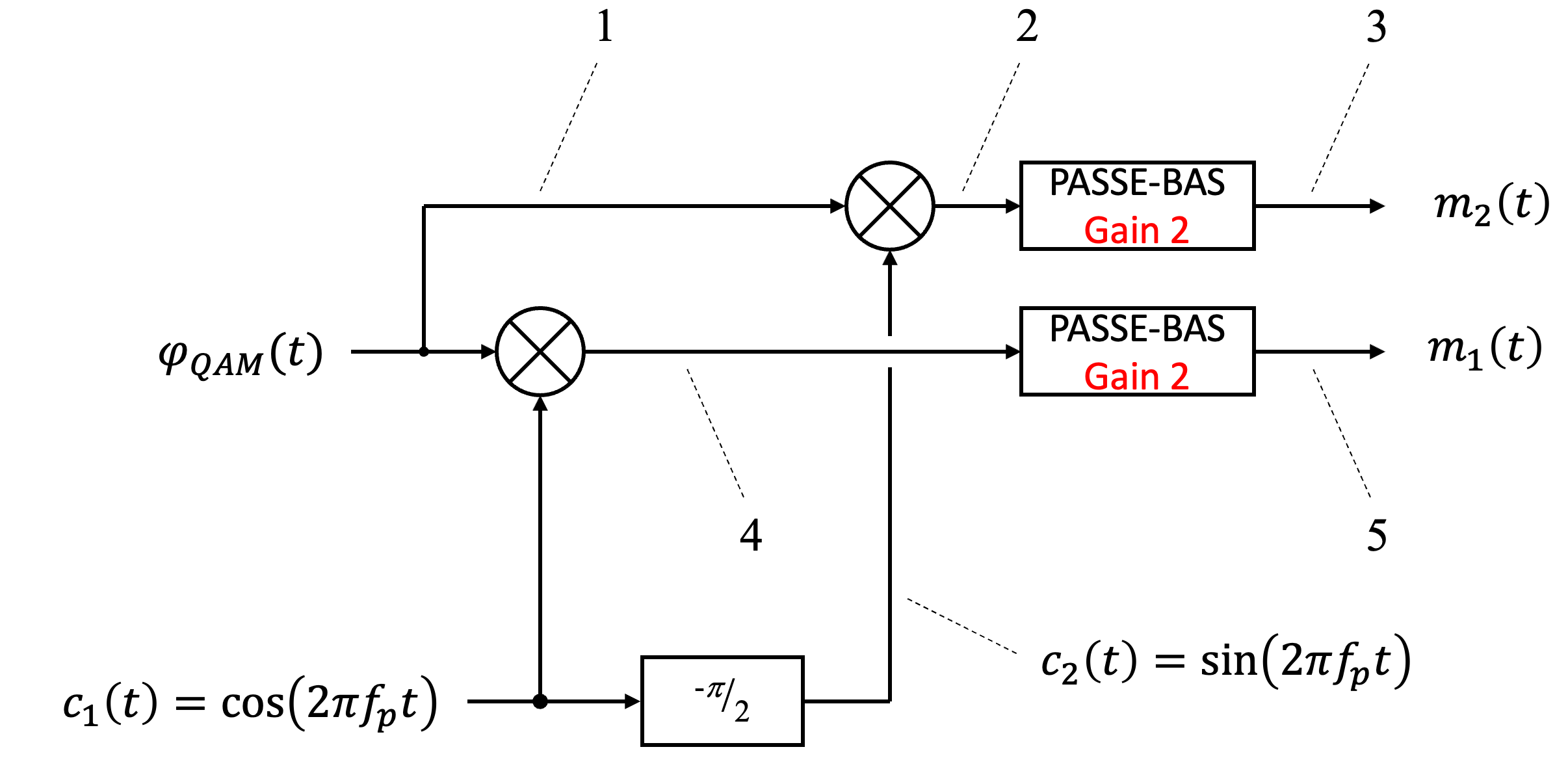
Figure 22:Démodulation cohérente de la QAM : séparation des signaux et en utilisant des porteuses en quadrature et un filtrage passe-bas.
La démodulation cohérente de la QAM-A consiste à extraire les deux signaux modulants et en utilisant des signaux de référence synchrones. Ce procédé repose sur le produit du signal reçu avec les mêmes porteuses utilisées lors de la modulation, suivi d’un filtrage passe-bas.
Le signal reçu est
Multiplication avec donne
Après filtrage passe-bas, gain de 2, on obtient
En plus, la multiplication avec
et après filtrage passe-bas (gain de 2) on a
Donc chaque signal modulant est extrait grâce aux signaux de référence synchrones et au filtrage passe-bas qui supprime les fréquences élevées. Notez que cette méthode nécessite une parfaite synchronisation pour éviter les interférences entre les deux canaux.
Modulation d’angle (analogique)¶
La modulation d’angle est une technique de modulation dans laquelle l’angle de la porteuse est modifié en fonction du signal message, comme noté dans (5). Elle inclut deux types principaux :
Modulation de fréquence (FM) où la fréquence instantanée varie proportionnellement au signal modulant.
Modulation de phase (PM) où la phase de la porteuse est directement influencée par le signal modulant.
Nous avons besoin de la notion de fréquence instantanée pour pouvoir définir les types de modulation d’angle.
- Définition: Fréquence instantanée (instantaneous frequency)
- Considerons un signal modulé, , la fréquence instantanée d’un signal modulé est donnée par :
où représente la phase du signal modulé.
Modulation de Fréquence (Frequency modulation; FM)¶
Dans la modulation de fréquence, l’expression du signal modulé est donnée par :
où est l’amplitude du signal modulé, est la fréquence porteuse, est le coefficient de sensibilité en fréquence [Hz/V], est le signal modulant (signal de message).
La fréquence instantanée du signal modulé est définie par :
La déviation maximale de fréquence est donnée par :
Modulation de Phase (Phase modulation; PM)¶
Dans la modulation de phase, l’expression du signal modulé s’écrit :
où est le coefficient de sensibilité en phase.
La fréquence instantanée est :
La déviation de fréquence maximale est alors donnée par :
Analyse Spectrale de la FM¶
L’analyse spectrale de la modulation de fréquence (FM) est essentielle pour comprendre la répartition de l’énergie du signal modulé en fréquence. Tout d’abord, définissons la fonction de Bessel.
Soit un signal modulant sinusoïdal :
Le signal FM correspondant est donné par :
où est la fréquence porteuse, est la fréquence du signal modulant, et β est l’indice de modulation.
L’équation du signal FM peut être exprimée sous forme de série de Bessel :
Cela montre que le spectre FM est composé d’un ensemble de fréquences discrètes, situées à :
avec des amplitudes pondérées par les fonctions de Bessel .
La densité spectrale du signal FM est obtenue par :
Cette équation signifie que l’énergie du signal est répartie sur plusieurs raies spectrales au lieu d’être concentrée sur une seule fréquence.
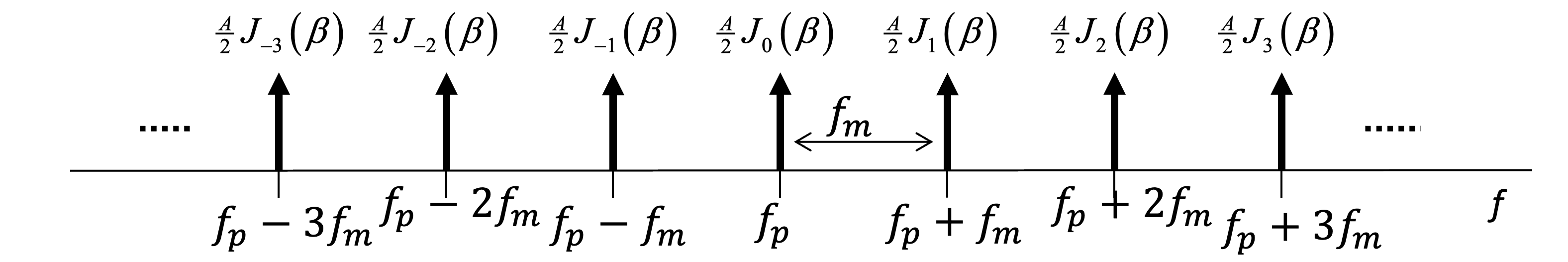
Figure 27:Spectre du signal FM de (65). raies spectrales situées aux fréquences , avec des amplitudes pondérées par les fonctions de Bessel
L’illustration montre les composantes spectrales aux différentes fréquences multiples de , avec des amplitudes proportionnelles aux valeurs des fonctions de Bessel . Cette analyse est essentielle pour la conception de systèmes de communication FM et pour comprendre leur occupation spectrale. Notez que la bande passante théorique des signaux FM est infinie; cependant, elle est approximée selon la règle de Carson ci-dessous.
-Règle de Carson
La règle de Carson fournit une estimation pratique de la bande passante des signaux FM et PM en fonction de l’indice de modulation β, évitant ainsi l’hypothèse d’une bande passante infinie.
Pour la modulation de fréquence (FM), la bande passante est donnée par :
où l’indice de modulation β est défini comme :
Pour la modulation de phase (PM), la bande passante suit une expression similaire :
avec :
- Démodulation d’un Signal FM

Figure 28:Démodulation d’un signal FM par détection d’enveloppe après dérivation
La démodulation de la FM repose sur l’extraction du signal modulant à partir du signal reçu. Une approche classique consiste à utiliser un détecteur basé sur la dérivation suivie d’une détection d’enveloppe.
Un signal modulé en fréquence s’écrit sous la forme :
où est la fréquence porteuse et représente le coefficient de sensibilité en fréquence.
La dérivée du signal FM est donnée par :
Cette expression met en évidence que l’amplitude de la fonction sinus est proportionnelle à la fréquence instantanée du signal.
Le processus de démodulation ppour la FM suit les étapes suivantes :
Dérivation : L’application d’un dérivateur permet de transformer les variations de fréquence en variations d’amplitude. L’amplitude de la sortie est proportionnelle à la fréquence instantanée :
Détection d’enveloppe : L’amplitude extraite par le dérivateur est ensuite récupérée à l’aide d’un détecteur d’enveloppe qui permet de retrouver le signal modulant .
Modulation numérique¶
La modulation numérique peut être utilisée lorsque la source est numérique. Elle permet de convertir une séquence de bits en un signal modulé adapté à la transmission sur un canal de communication. Nous pouvons également utiliser la modulation numérique à la sortie d’un modulateur par impulsions codées (PCM).
Dans un système de communication numérique, le flux de bits représente une séquence temporelle de valeurs binaires ( et ) qui doit être convertie en un signal physique pour la transmission. Ce flux peut être exprimé sous forme mathématique en utilisant une somme de fonctions impulsionnelles centrées sur les instants de temps où chaque bit est transmis. Le signal correspondant au flux de bits peut être modélisé comme :
où est la valeur du -ième bit, appartenant à l’ensemble , est la période de bit (l’intervalle de temps entre deux bits consécutifs), et finalement est l’impulsion de Dirac, utilisée pour représenter un signal discret en un ensemble d’impulsions temporelles.
Modulation numérique sans porteuse¶
Nous commencerons la discussion par la transmission binaire, qui permet de générer deux symboles distincts. Pour utiliser la modulation numérique, il est indispensable d’employer un codeur de symboles. Dans le cas binaire, cela implique deux symboles distincts. Nous représenterons le nombre de symboles par .
- Définition: Codeur de symboles
- Un codeur de symboles regroupe les bits ( ou ) en séquences appelées symboles (en Volts), où chaque symbole peut représenter un ou plusieurs bits en fonction du schéma de modulation utilisé.
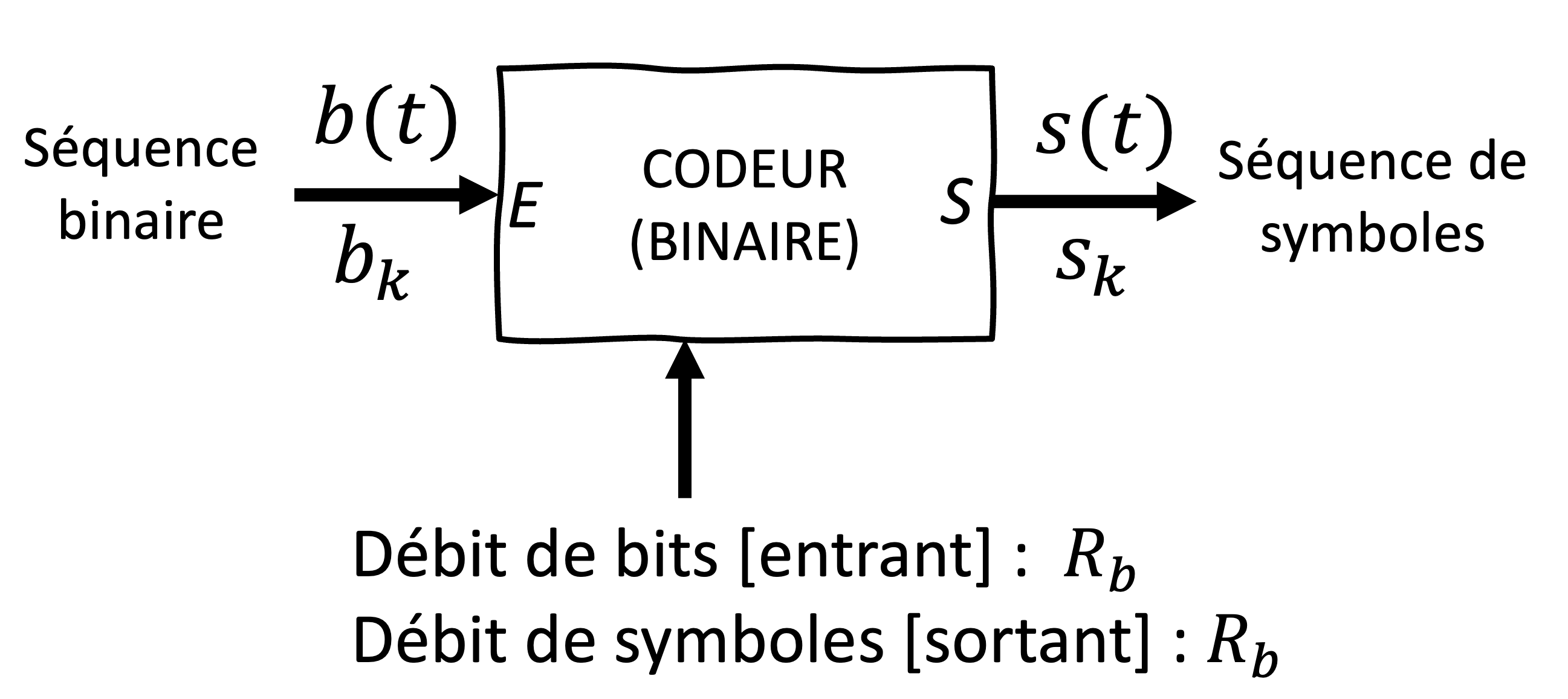
Figure 32:Le schéma représente un codeur de symboles qui transforme une séquence binaire en symboles (). L’entrée du codeur est une séquence de bits , qui est ensuite transformée en un ensemble de signal de sortie , correspondant à des symboles spécifiques utilisés pour la transmission. Ce processus est essentiel dans les systèmes de communication numérique pour adapter les données binaires à un format compatible avec une modulation spécifique.
Pour les codeurs de symboles binaires (), le signal de sortie, composé de symboles toutes les
2-PAM « Binary Pulse Amplitude Modulation »¶
La modulation d’amplitude par impulsions binaire (Binary Pulse Amplitude Modulation ; 2-PAM) est une technique de Modulation numérique binaire sans porteuse dans laquelle l’amplitude d’une impulsion est modulée en fonction d’un signal binaire. Cela signifie que les symboles transmis ne prennent que deux niveaux distincts, généralement associés aux bits et .
Le signal modulé en 2-PAM peut être exprimé comme suit :
où le codeur de symboles est
| (Bit d’entrée [Binaire]) | (Symbole de sortie [Tension]) |
|---|---|
| Volts | |
| Volts |
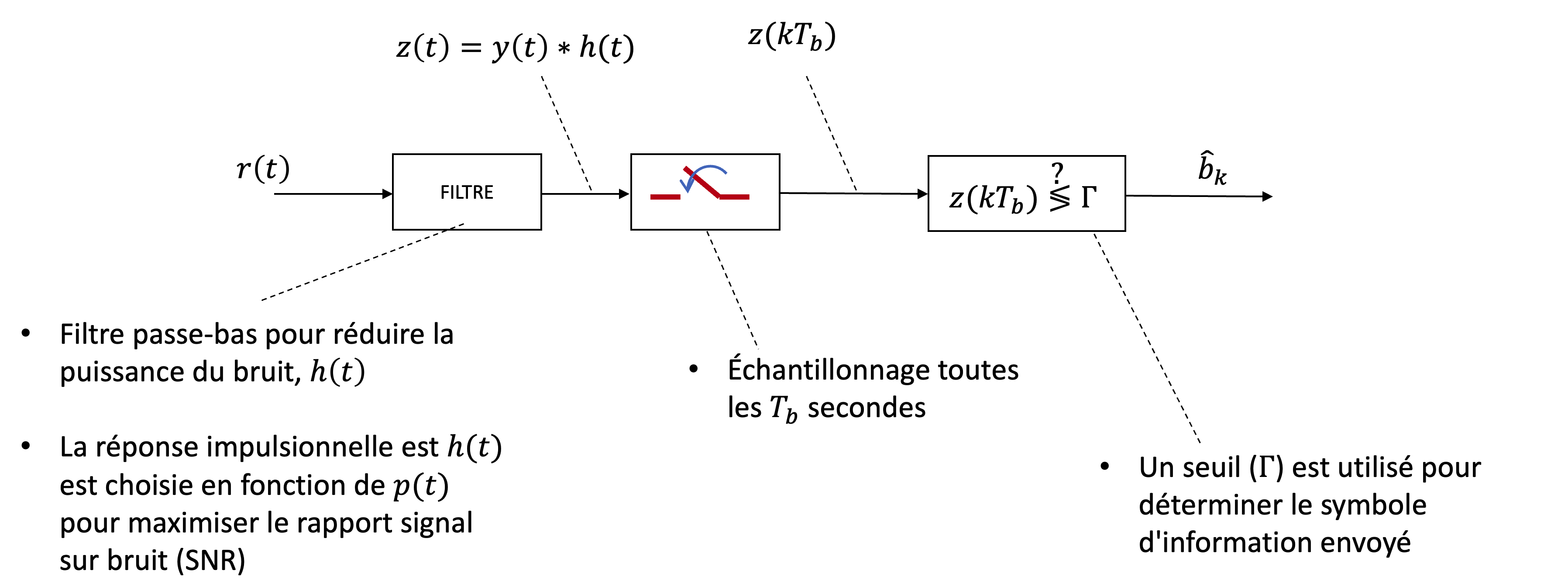
Figure 35:Schéma de réception d’un signal PAM : filtrage pour réduire le bruit, échantillonnage aux instants TbTb
Le récepteur PAM doit extraire l’information binaire du signal reçu. Le signal reçu est souvent bruité après la transmission.
où ( n(t) ) est le bruit ajouté par le canal. Un filtre passe-bas compatible avec la forme de l’impulsion (matched filter) est appliqué au est utilisé pour atténuer le bruit et limiter l’interférence entre les impulsions/ Le signal filtré est échantillonné à des intervalles de temps , correspondant aux instants où chaque impulsion doit être détectée :
Le récepteur applique une règle de décision pour déterminer si le symbole reçu correspond à un ou un . Une comparaison avec un seuil est effectuée :
où est la décision du récepteur. La synchronisation est nécessaire pour assurer l’alignement correct des échantillons avec les impulsions transmises.
Modulation numérique - -aire - sans porteuse¶
Pour augmenter le débit de bits, nous pouvons envoyer plus de deux symboles. Une approche consiste à l’utiliser symboles.
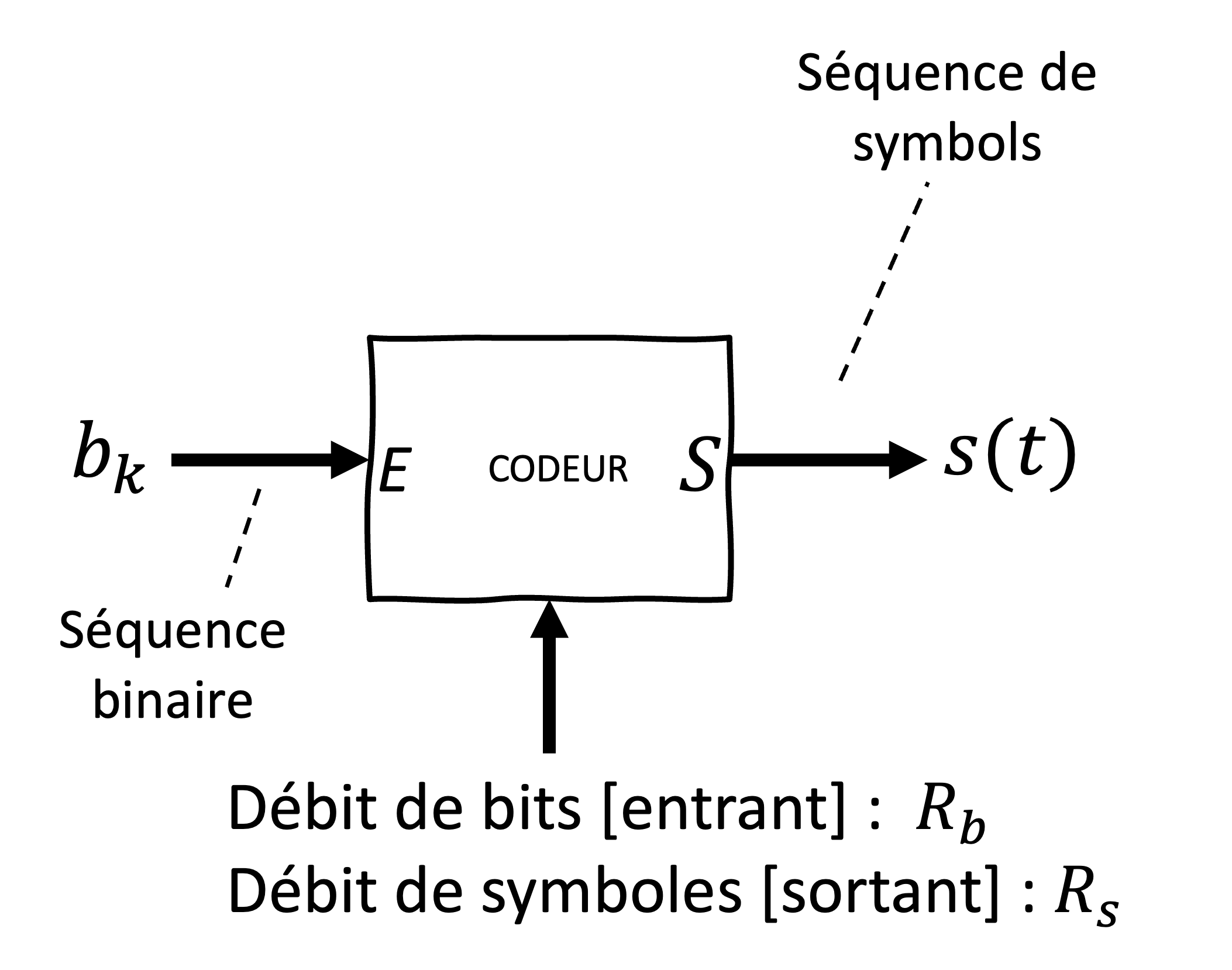
Figure 36:Le schéma représente un codeur de symboles qui transforme une séquence -aire en symboles. L’entrée du codeur est une séquence de bits , qui est ensuite transformée en un ensemble de signal de sortie , correspondant à des symboles spécifiques utilisés pour la transmission. Ce processus est essentiel dans les systèmes de communication numérique pour adapter les données binaires à un format compatible avec une modulation spécifique.
Le débit de bit entrant et le débit de symboles sortant peuvent varier en fonction du nombre total de symboles uniques, . Pour cette raison, deux indices temporels distincts sont utilisés :
- représente le -ième bit dans la séquence binaire d’entrée ().
- représente le -ième symbole en sortie du codeur de symboles ( et ).
Les principaux objectifs du codeur de symboles sont :
- Regrouper les bits en symboles pour s’adapter aux techniques de modulation utilisées.
- Améliorer l’efficacité spectrale, en adaptant le débit binaire au canal de transmission disponible.
- Faciliter la démodulation et la récupération des données à la réception.
M-PAM « M-ary Pulse Amplitude Modulation »¶
Le signal modulé en M-PAM (Modulation numérique - -aire - sans porteuse) peut être exprimé mathématiquement par :
où représente le symbole transmis appartenant à un ensemble de symboles distincts (), est la forme d’impulsion utilisée pour la transmission, et est la période de symbole, définissant l’intervalle de temps entre chaque transmission de symbole. Cette modulation permet de transmettre une quantité d’information plus importante par unité de temps par rapport à une modulation binaire classique.
Dans un système M-PAM, chaque symbole peut encoder plusieurs bits, avec un nombre de bits par symbole défini par :
La détection d’un signal modulé en M-PAM consiste à extraire les symboles transmis à partir du signal reçu. Ce processus implique plusieurs étapes essentielles permettant de minimiser les erreurs et d’optimiser la récupération de l’information.
Le signal reçu peut être modélisé comme :
où représente le bruit du canal. La première étape de détection consiste à appliquer un filtrage adapté pour maximiser le SNR. Le filtre optimal est choisi en fonction de , de manière à minimiser l’ISI.
Après le filtrage, le signal est échantillonné à des intervalles , produisant des valeurs discrètes :
où est le bruit affectant l’échantillon reçu.
Chaque échantillon est comparé aux niveaux de décision correspondant aux symboles possibles. Une règle de décision est appliquée en utilisant un détecteur à seuil pour déterminer le symbole reçu :
où sont les seuils de décision définis par :
Lorsque les signaux des messages sont aléatoires, nous devons utiliser leur spectre de densité de puissance, , pour déterminer sa largeur de bande.
Le bruit introduit dans le canal peut entraîner des erreurs lorsque le signal reçu est proche d’un seuil , conduisant à une probabilité d’erreur de symbole donnée par : où est la fonction de Q de Gauss, est la distance minimale entre deux niveaux de symboles, est la variance du bruit.
Modulation numérique avec porteuse¶
ASK « Amplitude Shift Keying »¶
ASK (modulation numérique - binaire - avec porteuse) est une technique dans laquelle l’amplitude d’une onde porteuse varie en fonction des données binaires à transmettre avec un codeur de symboles :
| (Bit d’entrée [Binaire]) | (Symbole de sortie [Tension]) |
|---|---|
| Volts | |
| Volts |
Le signal modulé en ASK peut être exprimé comme suit :
où est la porteuse utilisée pour la modulation.
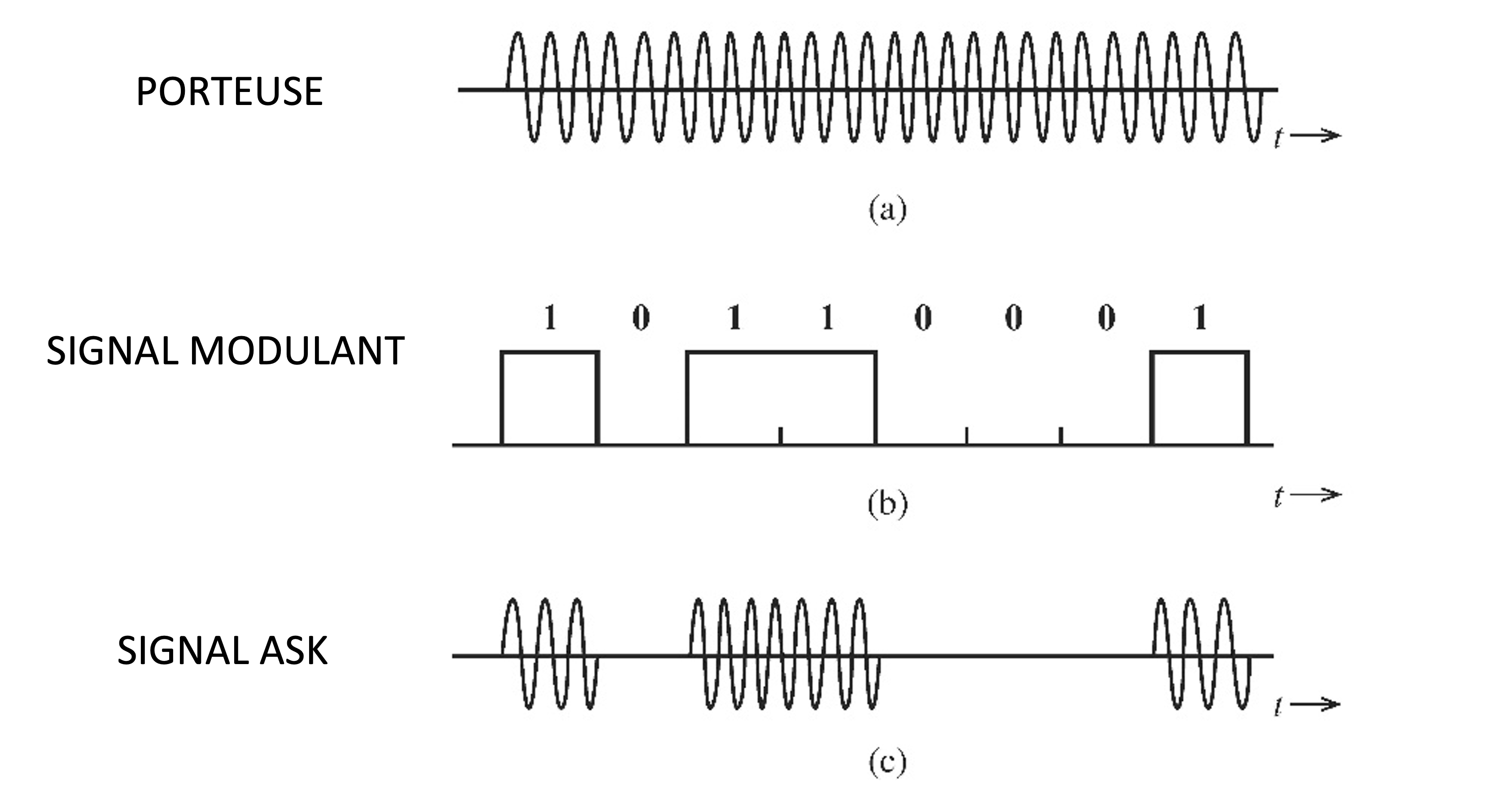
Figure 37:Dans la figure on peut observer ce processus en trois étapes distinctes. Une onde porteus est représentée comme un signal sinusoïdal continu, qui sera modulé en amplitude. Ensuite, la séquence binaire d’entrée est illustrée sous forme d’impulsions discrètes, correspondant aux bits transmis. Ces impulsions sont générées par le codeur de symboles, qui détermine comment chaque bit influencera le signal modulé. Enfin, la dernière partie de la figure montre le signal modulé en ASK, où la présence de la porteuse coïncide avec les bits 1, tandis que son absence correspond aux bits 0.
La démodulation du signal ASK consiste à extraire le signal modulant binaire à partir du signal reçu. Le signal reçu peut être exprimé sous la forme :
Pour récupérer l’information binaire, on multiplie le signal reçu avec la porteuse . Un filtre passe-bas compatible avec la forme de l’impulsion (matched filter) utilisé pour lisser le signal détecté et éliminer les hautes fréquences indésirables. Après filtrage, le signal obtenu est une version adoucie de l’enveloppe détectée. Le signal filtré est échantillonné à des intervalles de temps correspondant à la période des bits transmis,
Après la prise de décision, une séquence de bits est reconstruite. Ces bits correspondent aux données transmises avant la modulation ASK.
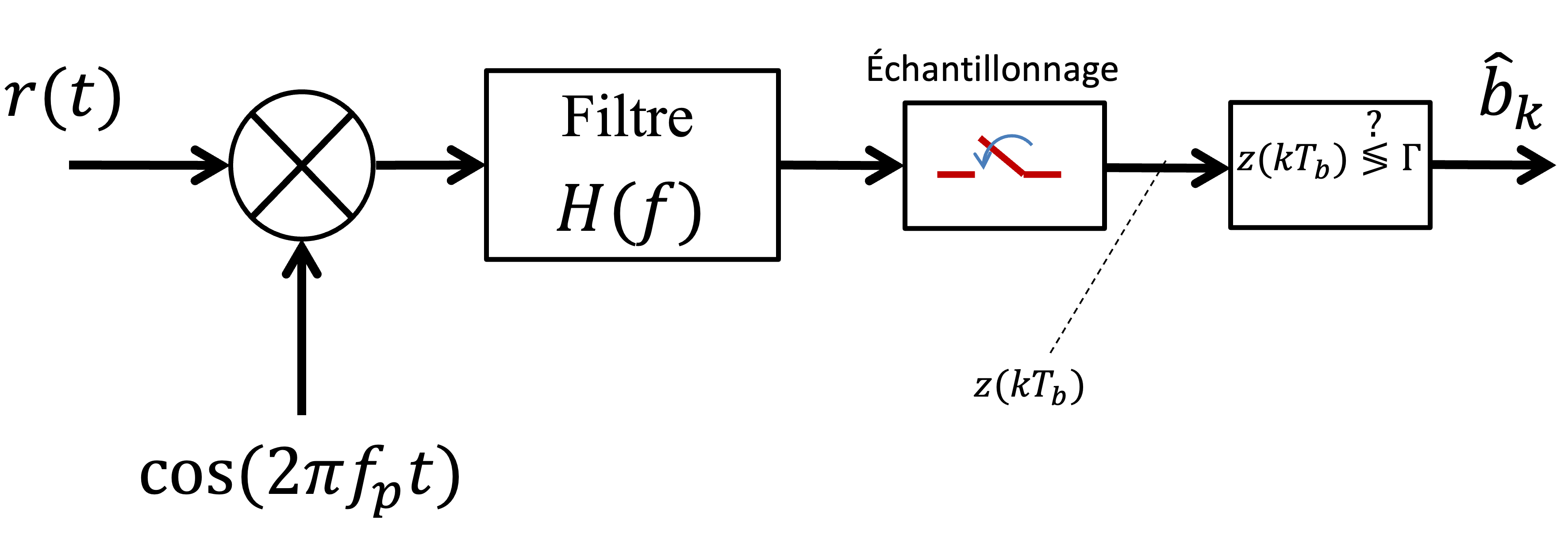
Figure 38:Schéma de démodulation cohérente d’un signal ASK, incluant la multiplication par la porteuse, le filtrage, l’échantillonnage et la prise de décision basée sur un seuil Γ.
Une constellation est utilisée pour la démodulation en associant chaque symbole reçu à l’un des points de la constellation. Après démodulation cohérente, le signal reçu est projeté sur la base d’onde , donnant :
et est ensuite comparé aux seuils de décision pour déterminer le symbole transmis . Ainsi, chaque point de la constellation permet une prise de décision robuste face au bruit, assurant une détection efficace du signal.
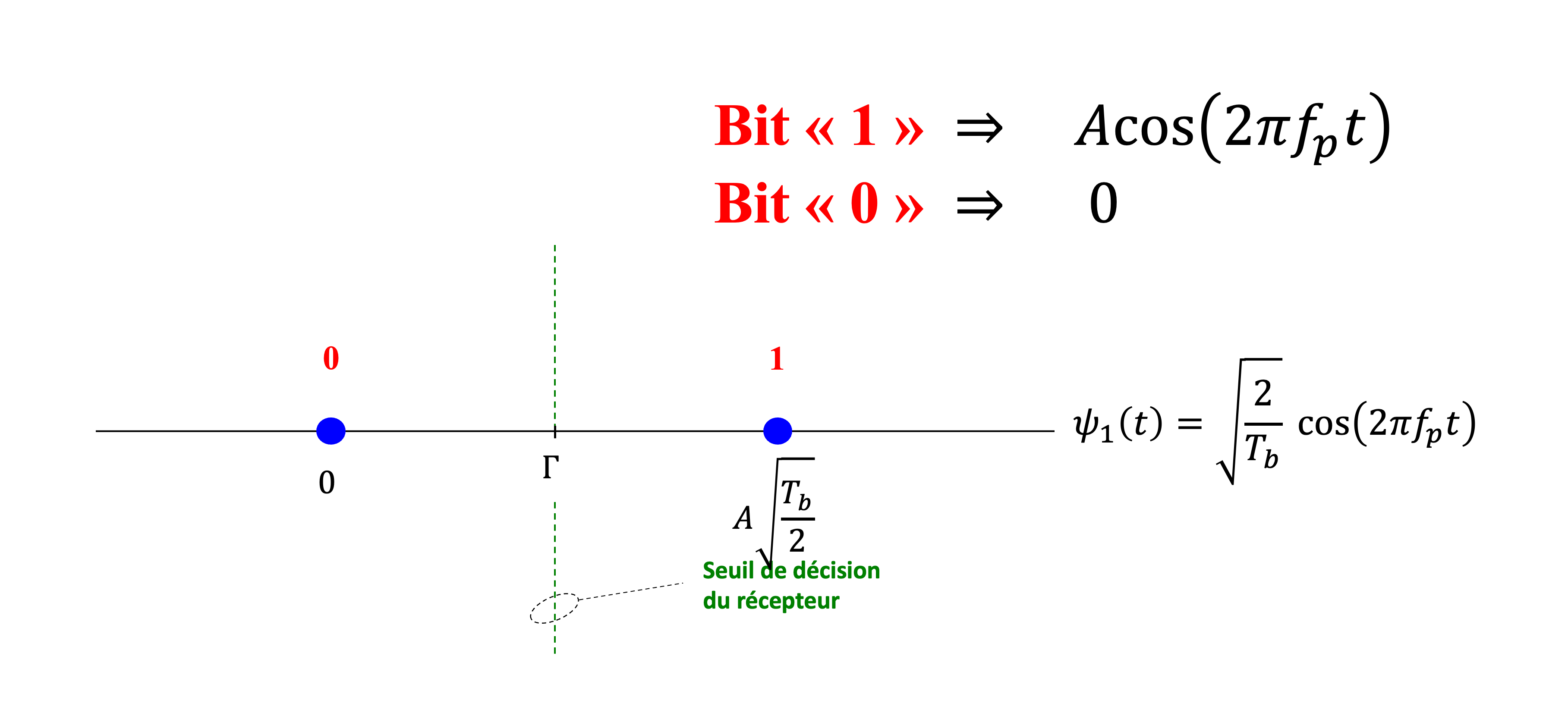
Figure 39:Constellation du ASK avec seuil de décision . Les bits \texttt{1} et \textbf{0} sont représentés par et respectivement.
PSK « Phase Shift Keying »¶
PSK (modulation numérique - binaire - avec porteuse) est une technique dans laquelle l’amplitude d’une onde porteuse varie sélon
| (Bit d’entrée [Binaire]) | (Symbole de sortie [Tension]) |
|---|---|
| Volts | |
| Volts |
et le signal modulé est écrit par
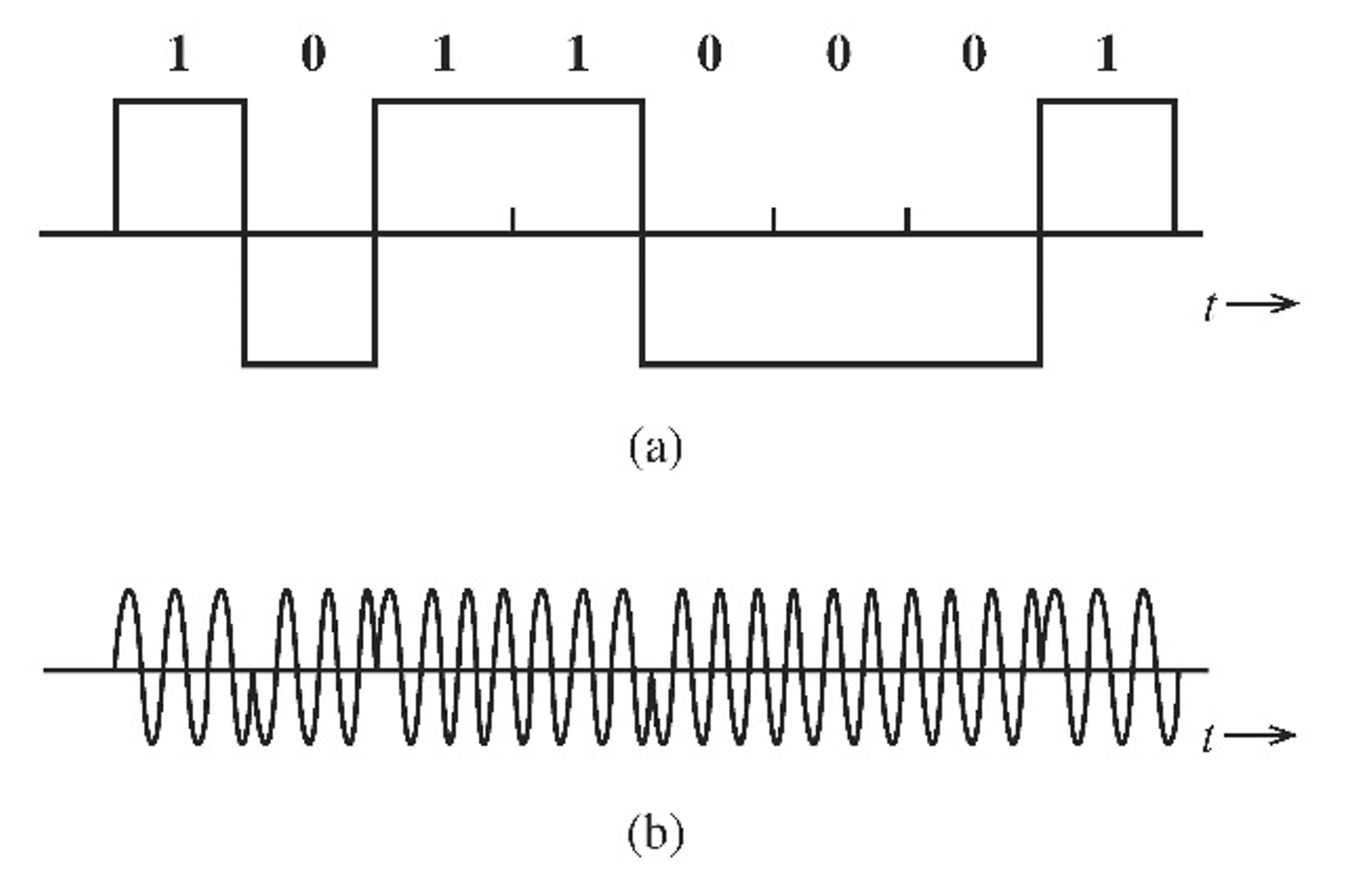
Figure 40:Signal binaire (a) et signal modulé en phase (b) illustrant la modulation PSK.
La même règle de détection s’applique, mais le seuil doit être choisi en fonction du codeur de symboles.
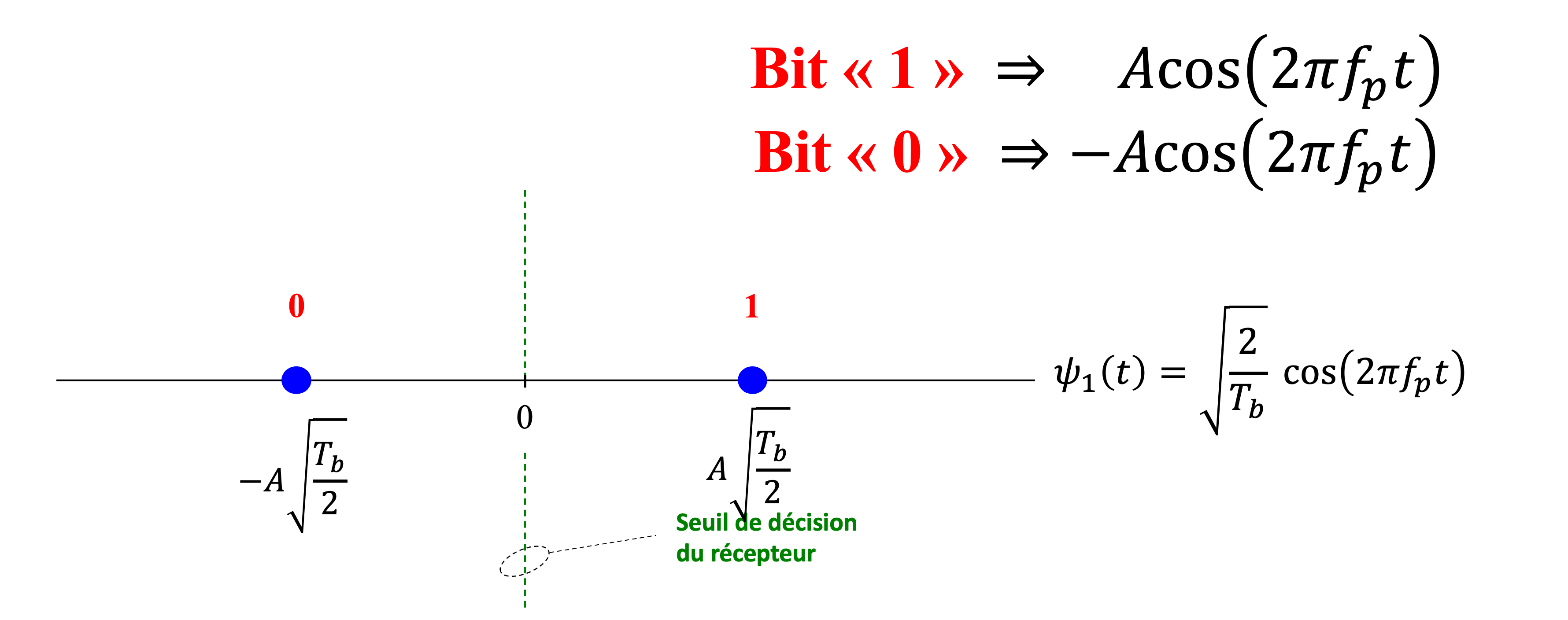
Figure 41:Constellation du BPSK avec seuil de décision Γ. Les bits et sont représentés par et respectivement.
QPSK « Quandrature Phase Shift Keying »»¶
QPSK (Quadrature Phase Shift Keying) (modulation numérique - -aire - avec porteuse) utilise deux porteuses en quadrature pour transmettre deux bits par symbole. Le signal modulé en QPSK est exprimé comme :
où et sont les sorties du codeur de symboles, représentant les deux bits modulés indépendamment sur les axes en phase (In-phase) et en quadrature (Quadrature). Les deux signaux modulés sont additionnés pour former le signal , qui peut transmettre deux bits par symbole, augmentant ainsi l’efficacité spectrale.
Les avantages du QPSK son l’efficacité spectrale améliorée (doublement du débit binaire par rapport au BPSK) et robustesse au bruit (car les symboles sont espacés de , réduisant les erreurs en présence d’interférences).
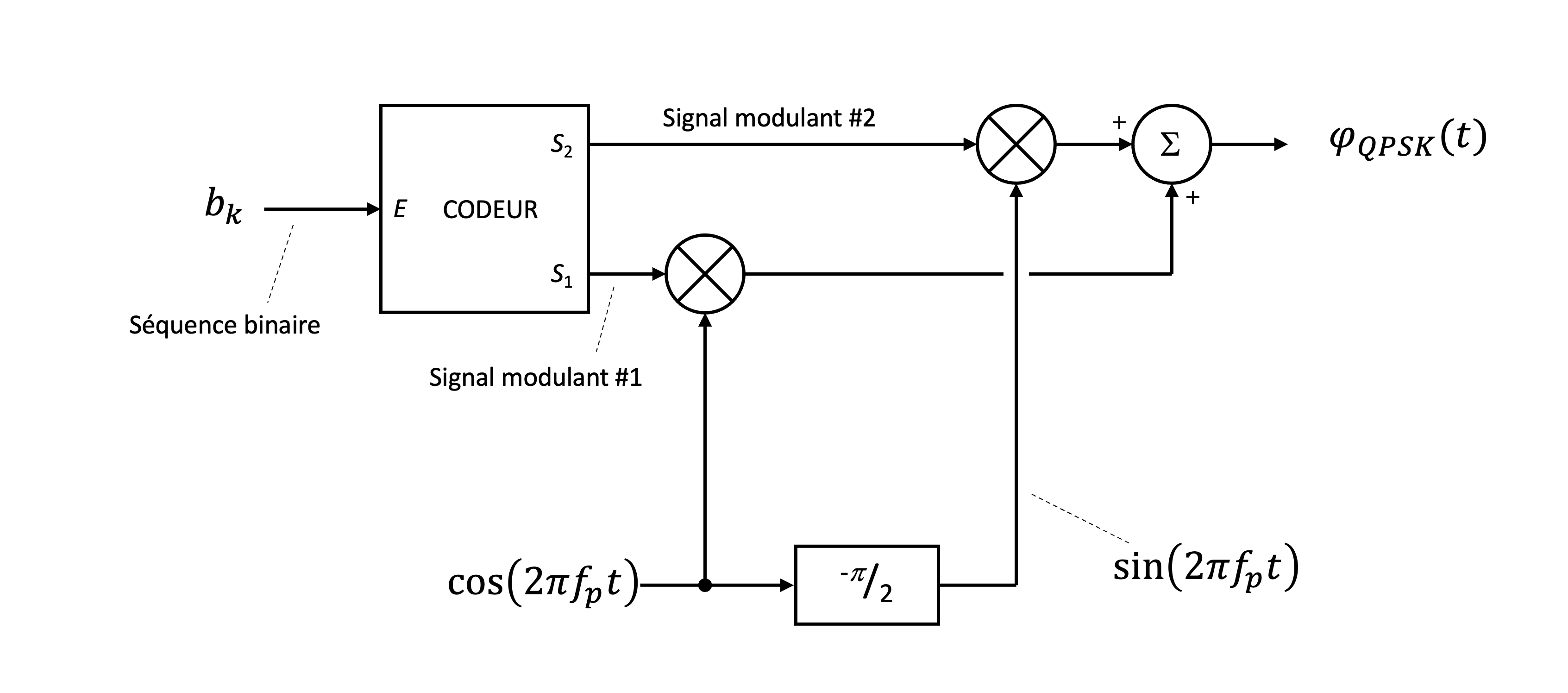
Figure 43:Schéma de modulation QPSK, combinant deux signaux modulants et sur des porteuses en quadrature et .
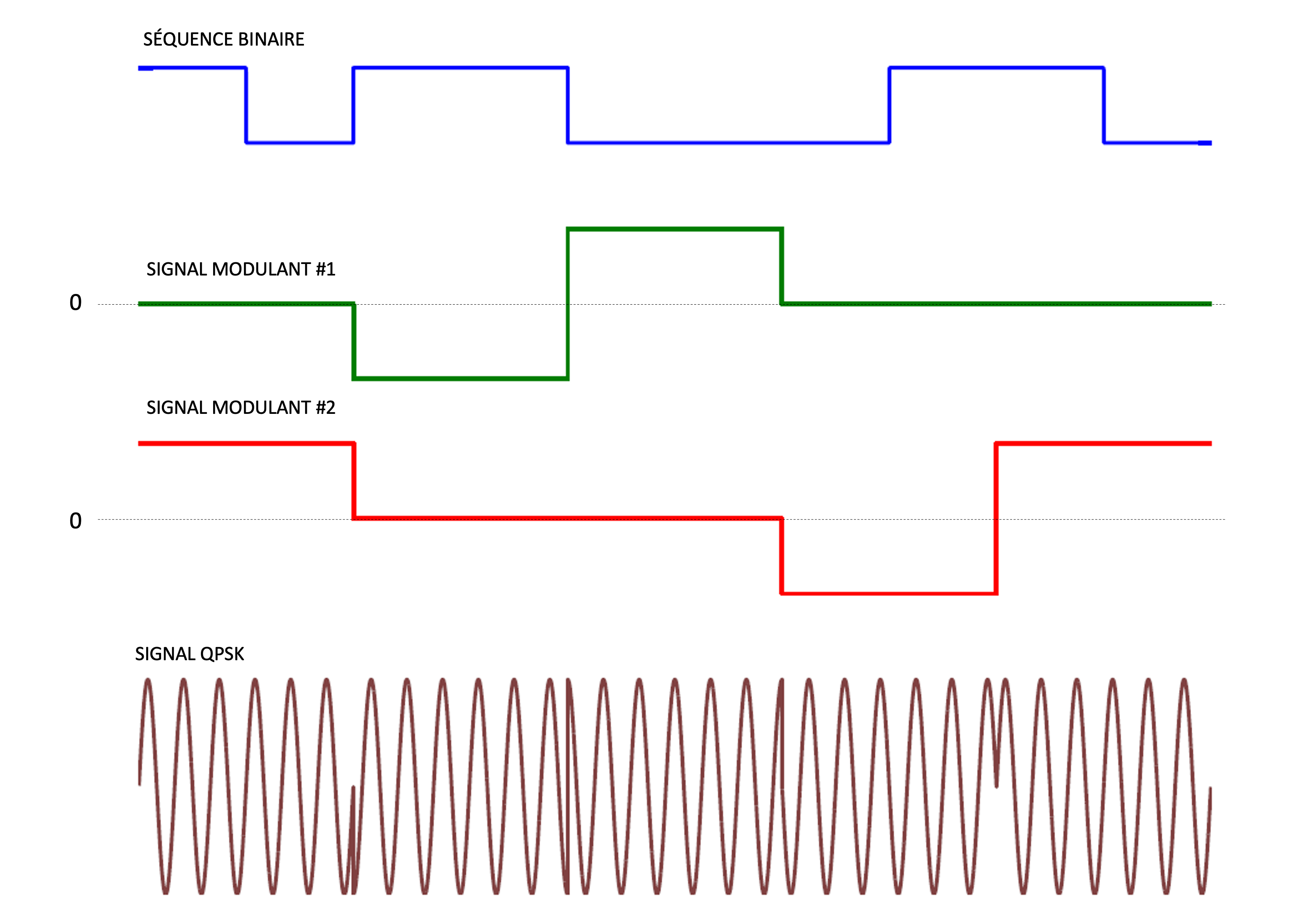
Figure 44:La figure illustre le processus de génération d’un signal modulé en QPSK (2 bits par symboles). La première courbe représente la séquence de bits d’entrée. Le premier signal modulant (courbe verte) est issu des bits pairs. Le second signal modulant (courbe rouge) est issu des bits impairs. module une porteuse en phase . module une porteuse en quadrature . L’addition des deux donne le signal modulé en QPSK.
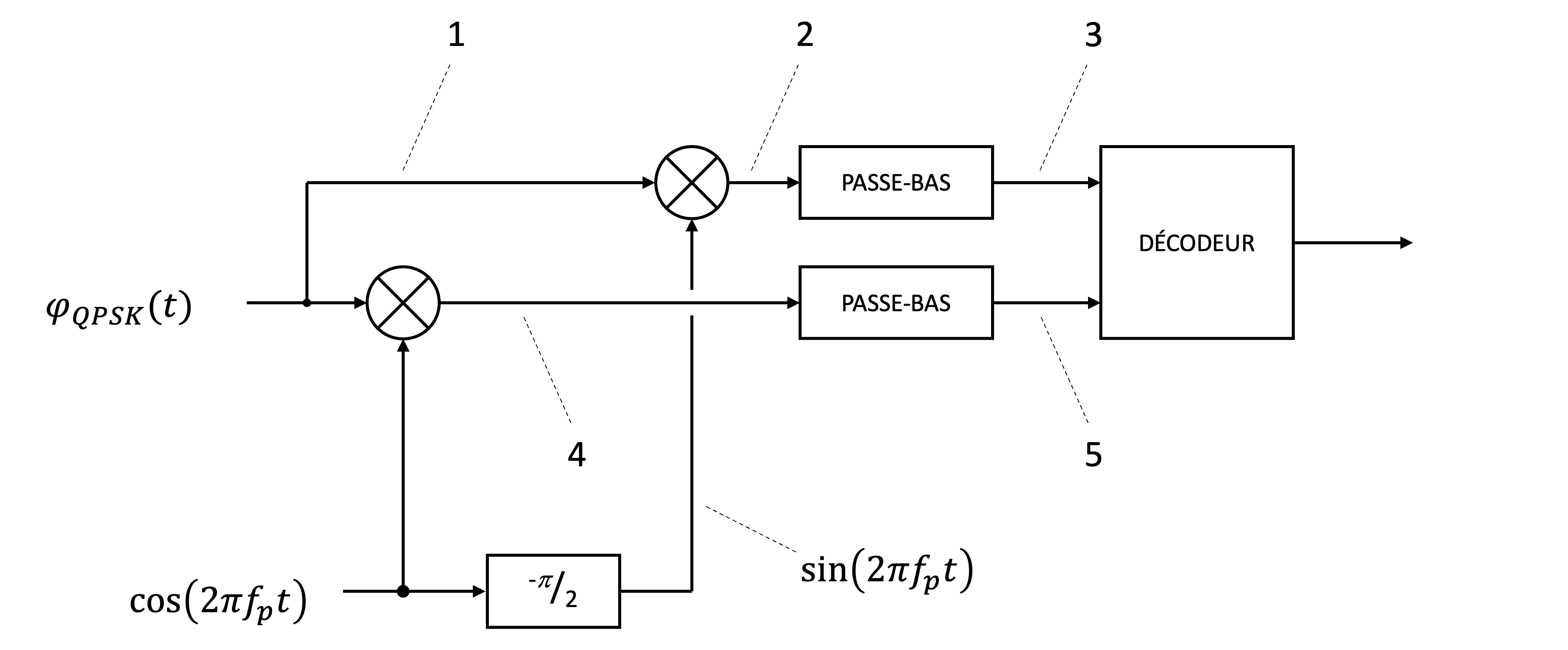
Figure 45:Schéma de démodulation du signal QPSK, utilisant des mélangeurs, des filtres passe-bas et un décodeur pour extraire les symboles transmis.
Pour la demodulation, le signal reçu est multiplié par deux signaux de référence : - Une porteuse en phase . - Une porteuse en quadrature , qui est obtenue en déphasant de . Après multiplication, chaque signal passe par un filtre passe-bas qui élimine les composantes haute fréquence et conserve uniquement les termes en bande de base.
Les signaux en sortie des filtres correspondent aux coefficients et , représentant les deux symboles. Ses valeurs sont comparées à un seuil pour déterminer les bits correspondants.
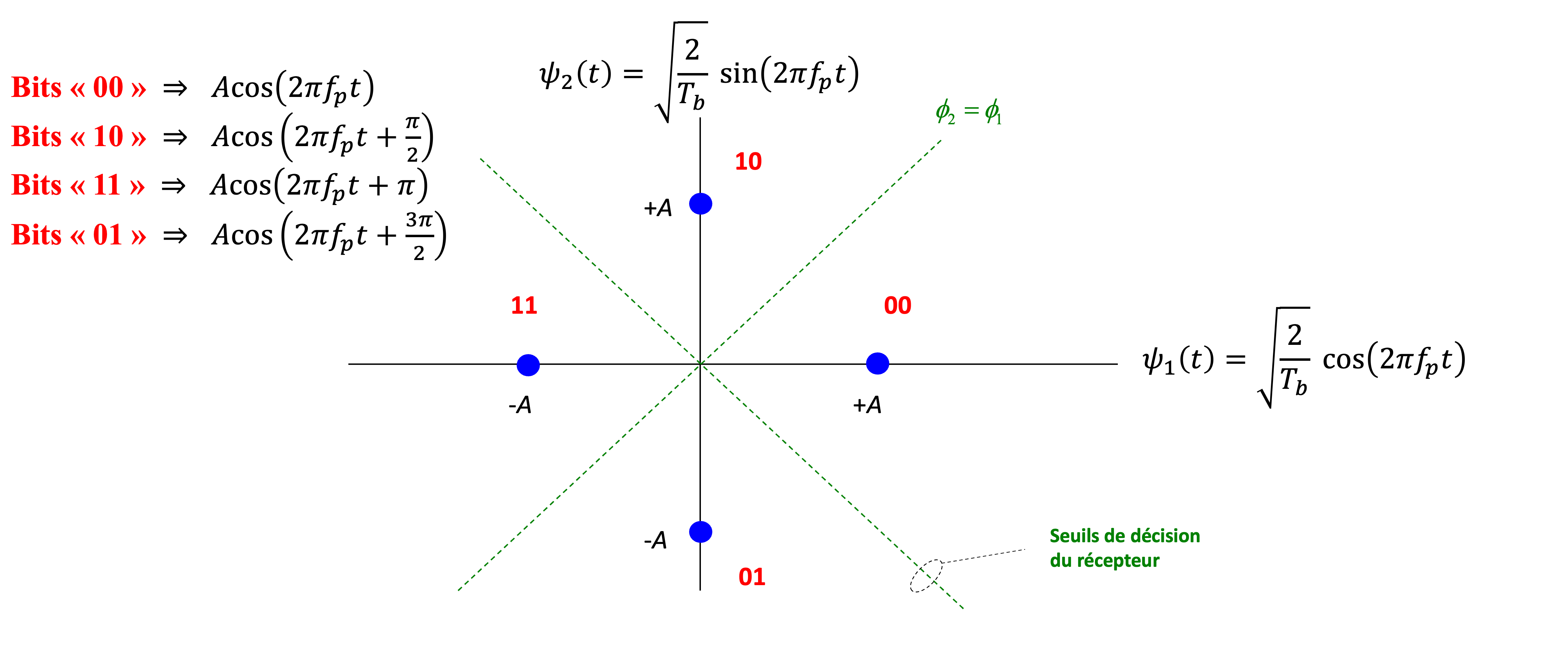
Figure 46:Constellation du QPSK avec seuils de décision pour la détection des symboles.
Resumé¶
Cette section traite de O4. Proposition des techniques de modulation appropriées en fonction des caractéristiques du canal et du type d’information, qui concerne l’encodage et de la modulation des signaux numériques. Elle explore la conversion des séquences binaires en séquences de symboles à l’aide de codeurs, la modulation d’amplitude et de phase (PAM, PSK, QPSK), ainsi que leur démodulation et détection via des constellations. L’impact du débit binaire et du débit symbolique sur les performances du système est également abordé.