Section 3 - Numérisation

Abstract¶

Cette section explore les bases de la numérisation des signaux, une étape clé dans les systèmes de communication modernes. Elle introduit tout d’abord les principes fondamentaux de l’échantillonnage, qui permettent de convertir un signal continu en une série d’échantillons discrets, garantissant ainsi une représentation fidèle selon le théorème de Nyquist-Shannon. Les applications pratiques de l’échantillonnage, notamment le calcul du débit maximal d’information et les modulations analogiques d’impulsions, y sont abordées. Ensuite, la section s’intéresse à la modulation par impulsions codées (Pulse Code Modulation; PCM), un processus crucial pour la transmission numérique des signaux. Les concepts de codage et de quantification sont détaillés pour expliquer comment les niveaux d’amplitude sont discrétisés en valeurs numériques. Enfin, la section conclut par une étude du multiplexage temporel, une technique permettant de partager efficacement un canal de communication entre plusieurs utilisateurs. Les principes de base et le format des trames sont explorés pour illustrer son importance dans les systèmes à grande échelle.

Introduction¶

La numérisation implique la transformation d’un signal du temps continu au temps discret (échantillonnage), puis en valeurs discrètes (quantification). La numérisation est réalisée par un convertisseur analogique-numérique (analog-to-digital converter; ADC). Sa performance généralement indiquée par la fréquence d’échantillonnage et le nombre de bits par échantillon. Le processus inverse, qui consiste à convertir un signal numérique en un signal continu, est effectué par un convertisseur numérique-analogique (digital-to-analog converter, DAC).

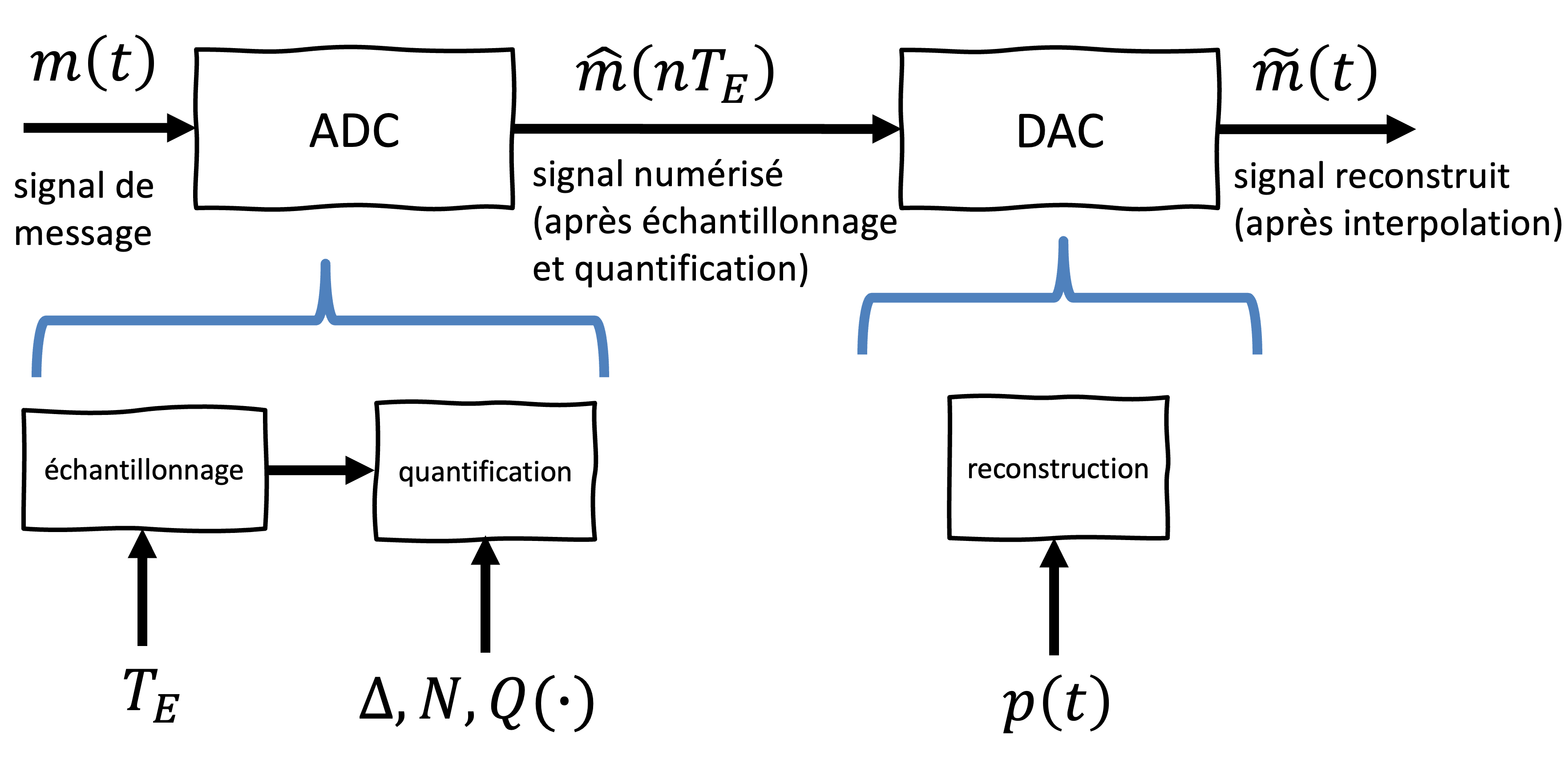
Schéma du processus de numérisation et de reconstruction d’un signal. Le signal analogique de message est d’abord converti en signal numérique via une conversion analogique-numérique (A/N), qui comprend l’échantillonnage à une période T_E et la quantification définie par \Delta, N, Q(\cdot) . Le signal numérisé est ensuite reconverti en signal analogique par une conversion numérique-analogique (N/A), où une interpolation est appliquée à l’aide de la fonction p(t) pour reconstruire une approximation du signal d’origine. — Figure 1:Schéma du processus de numérisation et de reconstruction d’un signal. Le signal analogique de message est d’abord converti en signal numérique via une conversion analogique-numérique (A/N), qui comprend l’échantillonnage à une période $T_E$ et la quantification définie par $\Delta, N, Q(\cdot)$ . Le signal numérisé est ensuite reconverti en signal analogique par une conversion numérique-analogique (N/A), où une interpolation est appliquée à l’aide de la fonction $p(t)$ pour reconstruire une approximation du signal d’origine.

Échantillonnage (Sampling)¶

Définition: Échantillonnage: L’échantillonnage est la lecture d’un signal, $m(t)$ à intervalles réguliers, $T_E$ seconds ( $T_E$ est la période d’échantillonnage). Donc on utilise une fréquence d’échantionnage de $f_E$ Hz. La problématique principale est liée à l’échantillonnage sans perdre d’information. Cela nous permet d’utiliser l’interpolation et de reconstituer le signal original. Nous représenterons le signal échantillonné comme $m_E(t)$ .

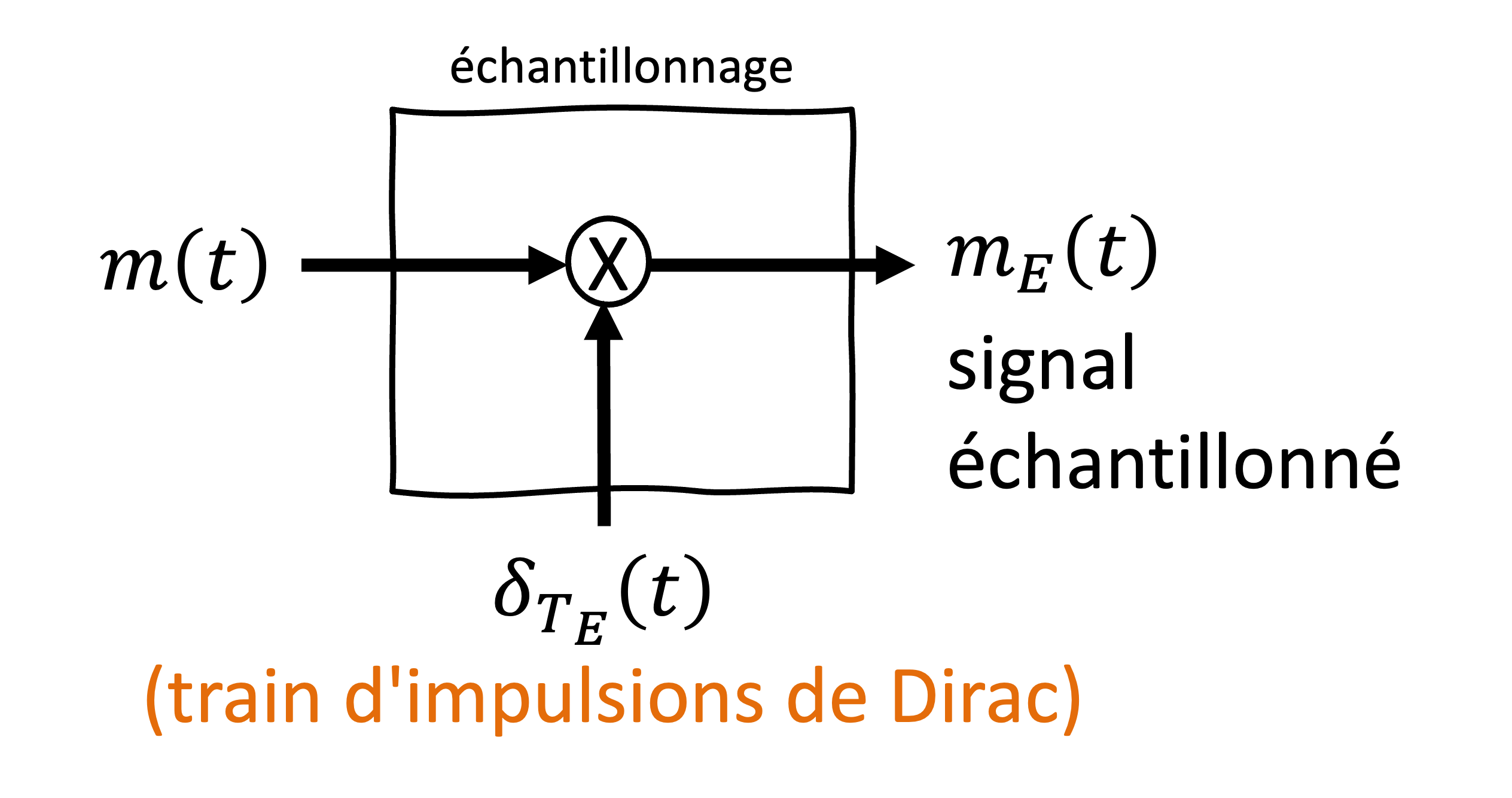
Schéma du processus d’échantillonnage d’un signal. Le signal analogique m(t) est multiplié par un train d’impulsions \delta_{T_E}(t) , représentant une suite de deltas de Dirac espacés de T_E. Cette opération produit le signal échantillonné m_E(t) , qui conserve les valeurs de m(t) aux instants d’échantillonnage. Ce processus est la première étape de la conversion analogique-numérique (A/N), garantissant une représentati on discrète du signal original. — Figure 2:Schéma du processus d’échantillonnage d’un signal. Le signal analogique $m(t)$ est multiplié par un **train d’impulsions** $\delta_{T_E}(t)$ , représentant une suite de deltas de Dirac espacés de $T_E$ . Cette opération produit le signal échantillonné $m_E(t)$ , qui conserve les valeurs de $m(t)$ aux instants d’échantillonnage. Ce processus est la première étape de la conversion analogique-numérique (A/N), garantissant une représentati on discrète du signal original.

Soit $m(t)$ un signal limité (dans le domaine des fréquences) à $B$ Hz. Le signal échantillonné est :

m_E(t) = m(t) \delta_{T_E}(t) = \sum_{n=-\infty}^{\infty} m(nT_E) \delta(t - nT_E)

(1)

où $\delta_{T_E}(t)$ représente un train d’impulsions de Dirac, défini comme (26), et $m(nT_E)$ représente la valeur de $m(t)$ à $t = nT_E$ sec. Sachant que

\delta_{T_E}(t) = \sum_{n=-\infty}^{\infty} \delta (t - nT_E) = \frac{1}{T_E} \sum_{n=-\infty}^{\infty} e^{j 2\pi n f_E t}

(2)

la transformée de Fourier de $g_E(t)$ peut être écrite comme

M_E(f) = M(f) * \frac{1}{T_E} \sum_{n=-\infty}^{\infty} \delta(f - n f_E) = \frac{1}{T_E} \sum_{n=-\infty}^{\infty} M(f - n f_E)

(3)

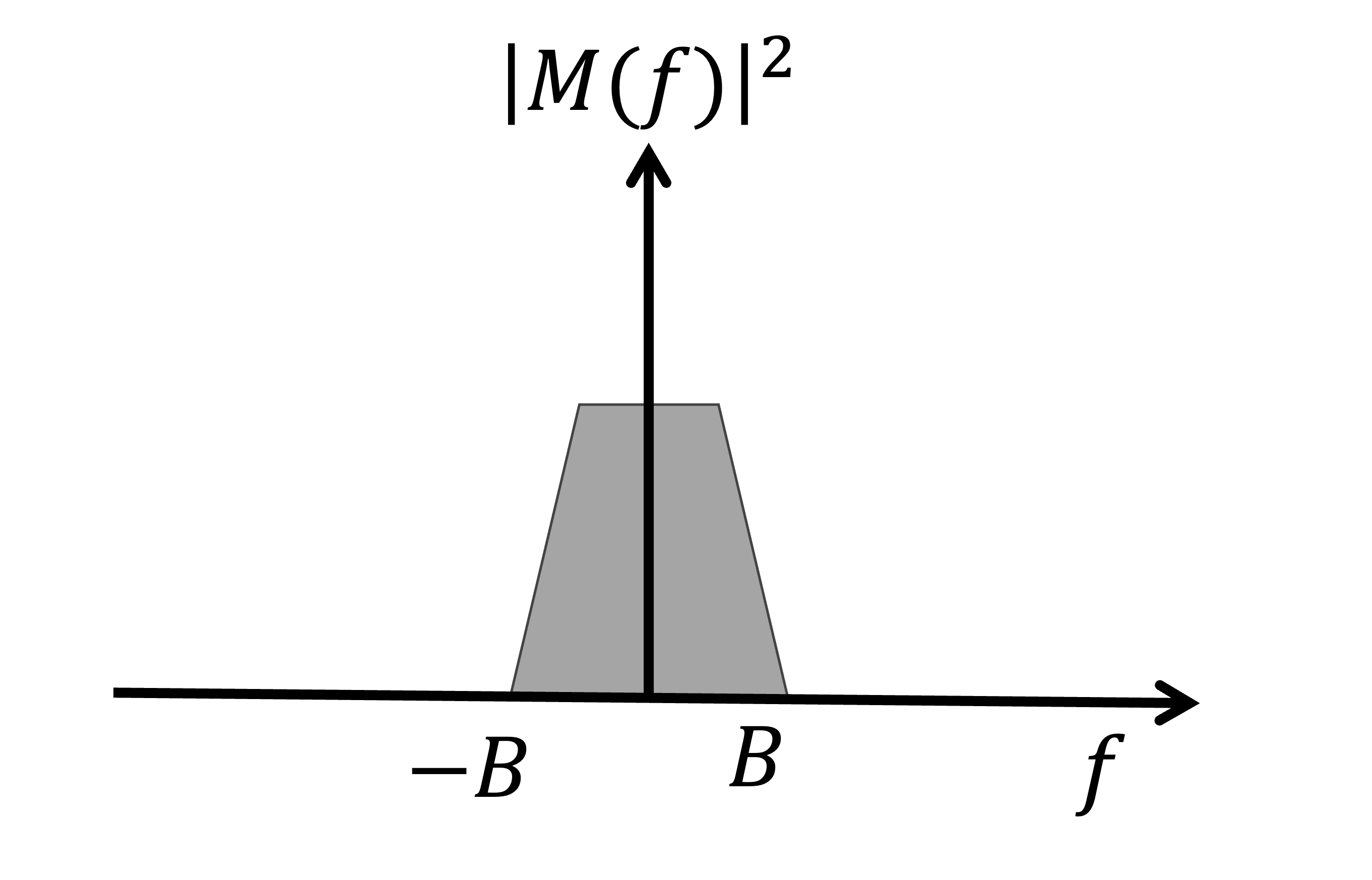
Un exemple de signal de message à bande limitée, B Hz. — Figure 3:Un exemple de signal de message à bande limitée, $B$ Hz.

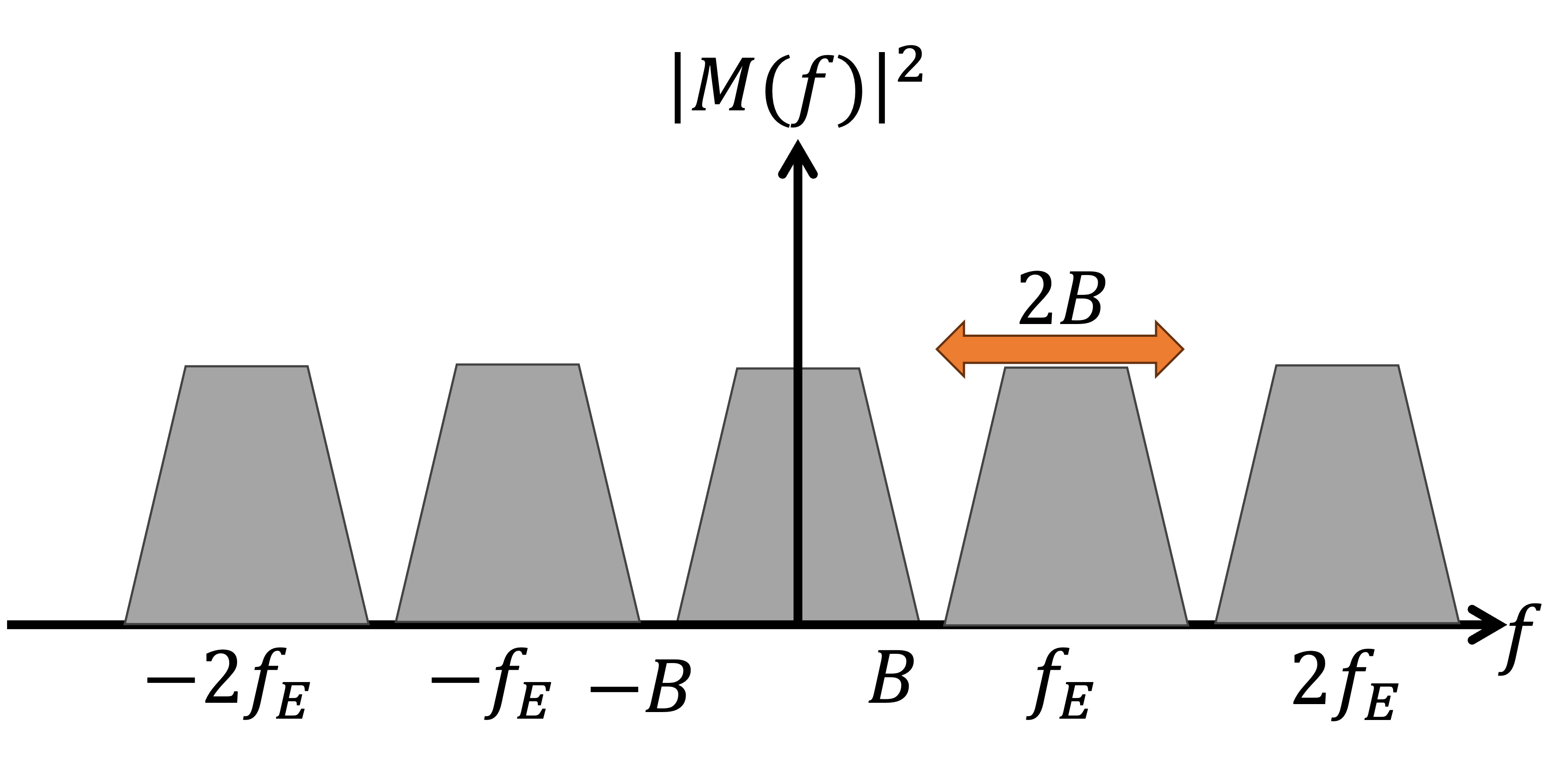
La version échantillonnée du signal dans le domaine fréquentiel devient périodique avec une fréquence f_E , qui est la fréquence d’échantillonnage. Tant que f_E > 2B , il n’y a pas de recouvrement (aliasing). Les copies peuvent rester non chevauchantes. — Figure 4:La version échantillonnée du signal dans le domaine fréquentiel devient périodique avec une fréquence $f_E$ , qui est la fréquence d’échantillonnage. Tant que $f_E > 2B$ , il n’y a pas de recouvrement (aliasing). Les copies peuvent rester non chevauchantes.

Reconstruction¶

Selon le théorème d’échantillonnage de Nyquist-Shannon, un signal, $m(t)$ dont le spectre est limité à une bande de fréquences comprise entre $-B$ et $B$ Hz peut être parfaitement reconstruit à partir de ses échantillons si et seulement si la fréquence d’échantillonnage $f_E$ respecte la condition

f_E \geq 2B

(4)

Le taux de Nyquist ( $2B$ ) est définie comme la fréquence minimale d’échantillonnage nécessaire pour éviter le chevauchement lors de la numérisation d’un signal. Donc le taux de Nyquist représente donc la fréquence d’échantillonnage minimale requise pour assurer une reconstruction fidèle du signal sans perte d’information.

Définition: chevauchement (aliasing): Nous devons nous conformer aux critères de Nquist, sinon nous observons un effet de chevauchement. Le chevauchement se produit lorsqu’un signal est échantillonné à une fréquence inférieure au taux de Nyquist ( $f_E < 2B$ ). Ce chevauchement entraîne une distorsion irréversible du signal, où différentes fréquences deviennent indiscernables.

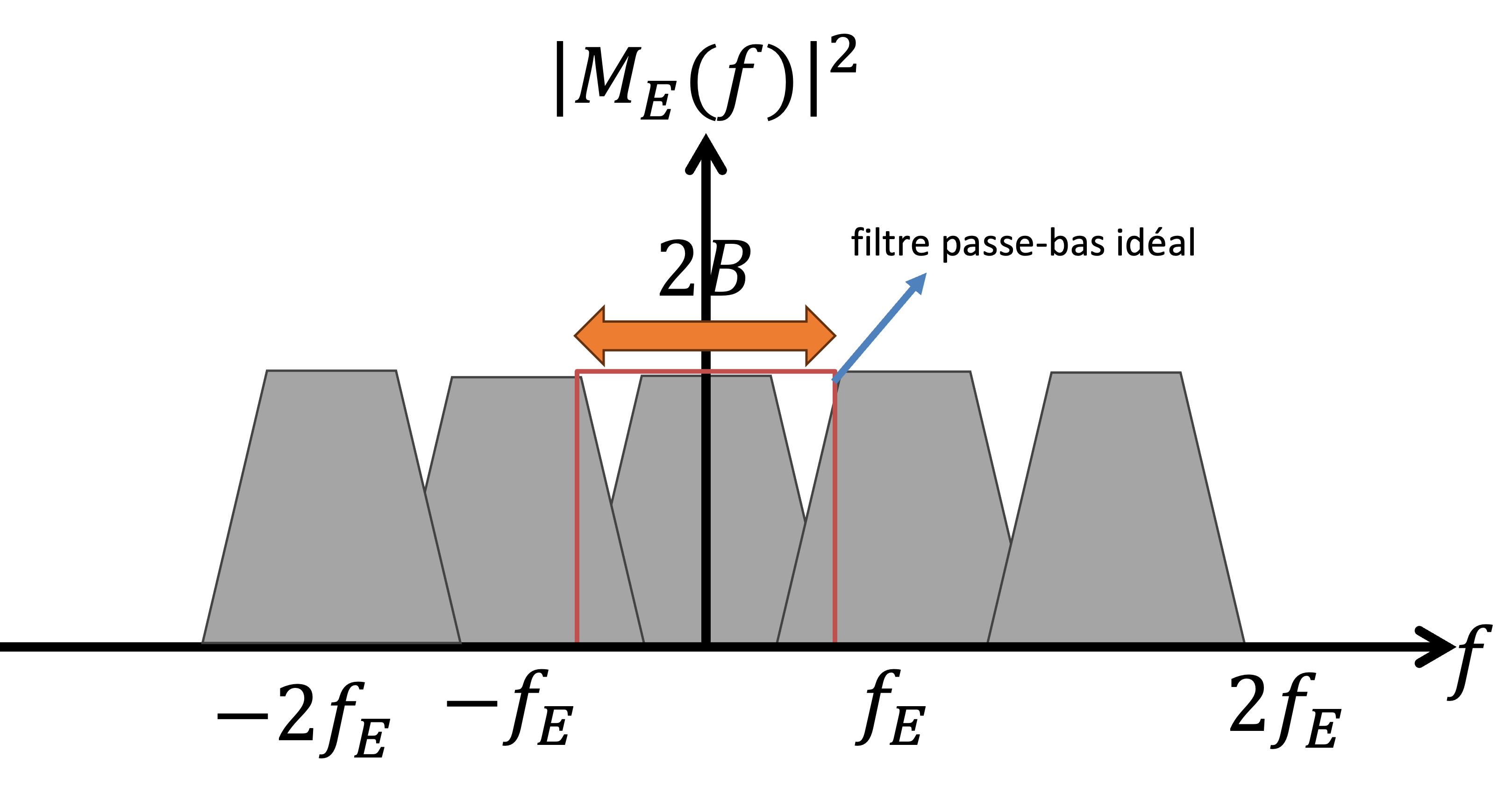
Une illustration du chevauchement (aliasing) (f_E < 2B) — Figure 5:Une illustration du chevauchement (aliasing) $(f_E < 2B)$

Reconstruction idéale¶

Si un signal $m(t)$ a été échantillonné avec une fréquence $f_E \geq 2B$ , la reconstruction idéale est réalisée en filtrant le spectre du signal échantillonné avec un filtre passe-bas idéal dont la réponse en fréquence est :

H(f) = T_E \cdot \prod \left( \frac{f}{2B} \right) = \begin{cases} T_E & \text{si } |f| \leq B \\ 0 & \text{si } |f| > B \end{cases}

(5)

où $\prod(x)$ représente une fonction porte qui sélectionne uniquement les fréquences comprises entre $-B$ et $B$ Hz. Ce filtre passe-bas idéal élimine les copies spectrales indésirables introduites lors de l’échantillonnage.

En domain temporel, $m(t)$ peut être parfaitement reconstruit par interpolation de sinc :

m(t) = \sum_{n=-\infty}^{\infty} m(nT_E) \text{sinc} \left( \frac{\pi(t - nT_E)}{T_E} \right)

(6)

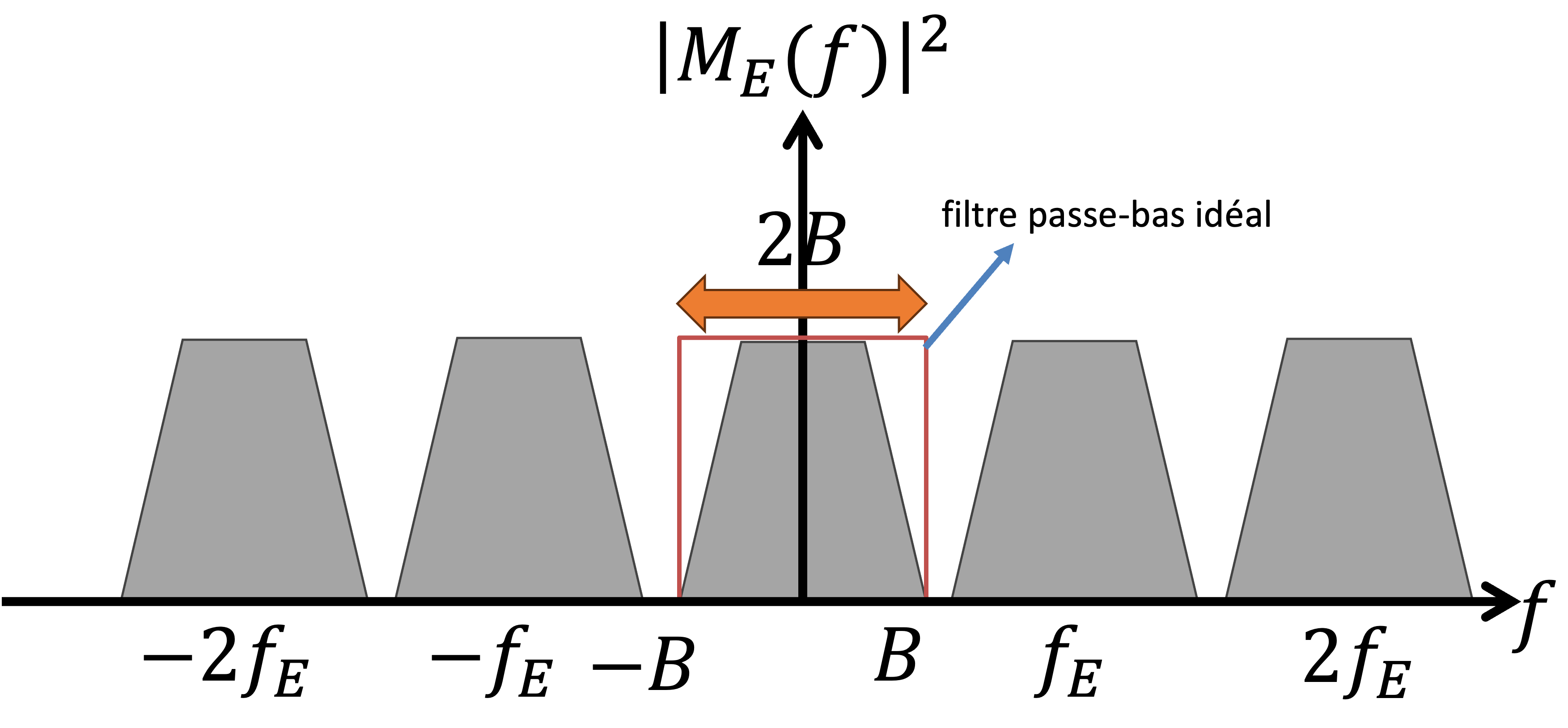
Un filtre passe-bas idéal est utilisé pour extraire la bande originale de largeur 2B, éliminant ainsi les répliques spectrales et permettant la reconstruction du signal initial. — Figure 6:Un **filtre passe-bas idéal** est utilisé pour extraire la bande originale de largeur $2B$ , éliminant ainsi les répliques spectrales et permettant la reconstruction du signal initial.

Reconstruction pratique (interpolation)¶

L’interpolation est le processus de reconstruction d’un signal continu à partir de ses échantillons discrets en utilisant un filtre passe-bas ayant une réponse impulsionnelle $p(t)$ .

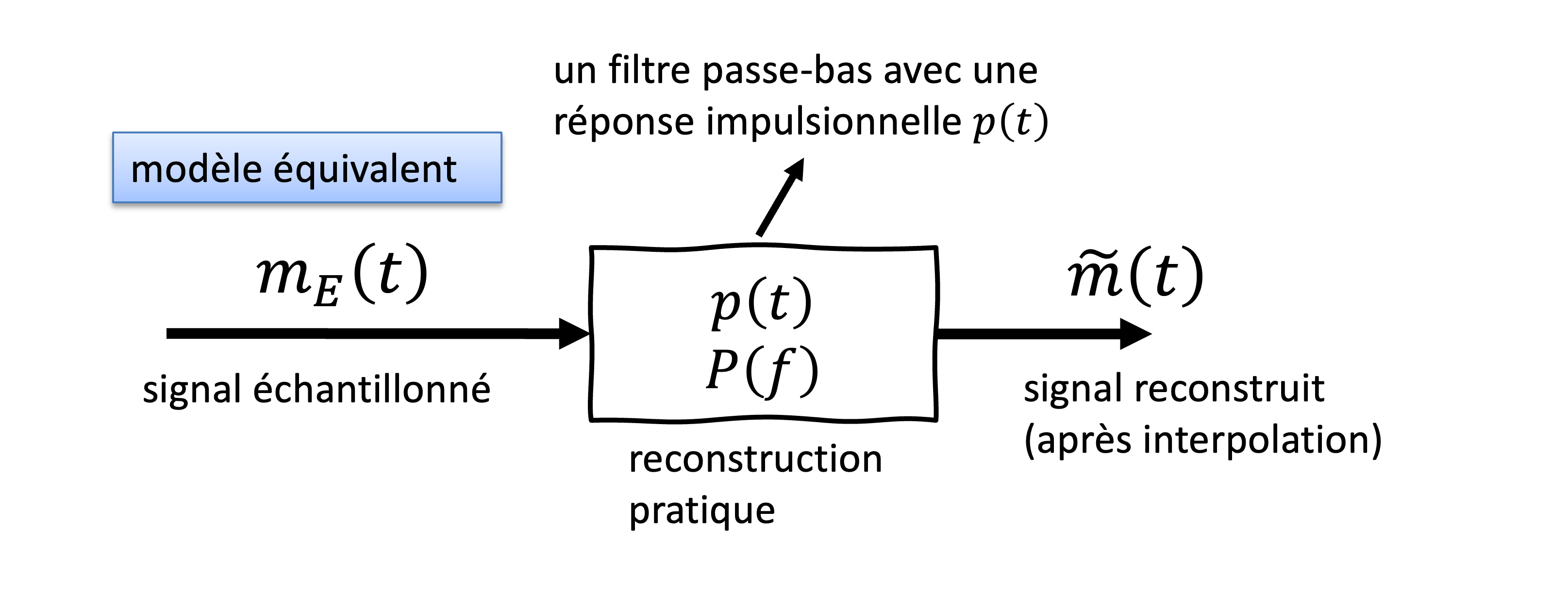
Modèle équivalent de reconstruction d’un signal échantillonné. Le signal échantillonné m_E(t)est filtré par un filtre passe-bas ayant une réponse impulsionnelle p(t) et une réponse en fréquence P(f) . Ce filtrage permet d’éliminer les répliques spectrales indésirables et de reconstruire une approximation du signal original, notée \tilde{m}(t) . Cette approche constitue une reconstruction pratique du signal après l’étape d’échantillonnage. — Figure 7:Modèle équivalent de reconstruction d’un signal échantillonné. Le signal échantillonné $m_E(t)$ est filtré par un **filtre passe-bas** ayant une réponse impulsionnelle $p(t)$ et une réponse en fréquence $P(f)$ . Ce filtrage permet d’éliminer les répliques spectrales indésirables et de reconstruire une approximation du signal original, notée $\tilde{m}(t)$ . Cette approche constitue une **reconstruction pratique** du signal après l’étape d’échantillonnage.

Lorsque nous ne pouvons pas créer un filtre idéal, nous pouvons utiliser un filtre pratique avec une réponse impulsionnelle $p(t)$ qui a une durée finie dans le temps, permettant une reconstruction approximative tout en réduisant la complexité de mise en œuvre. L’interpolation peut être vue comme un filtrage de convolution du signal échantillonné $m_E(t)$ avec un filtre passe-bas non-idéal avec une réponse impulsionnelle du filtre passe-bas $p(t)$ , qui permet de lisser les échantillons et de reconstruire un signal continu :

\widetilde{m}(t) = m_E(t) * p(t) = \sum_{n=-\infty}^{\infty} m(nT_E) p(t - nT_E)

(7)

où $\widetilde{m}(t)$ est le signal reconstruit et $*$ représente l’opération de convolution.

L’expression de la transformée de Fourier du signal reconstruit est donnée par :

\widetilde{M}(f) = M_E(f) P(f) = P(f) \frac{1}{T_E} \sum_{n=-\infty}^{\infty} M(f - n f_E)

(8)

où $\tilde{G}(f)$ est le spectre du signal reconstruit, $M_E(f)$ est le spectre du signal échantillonné, et $P(f)$ est la réponse en fréquence du filtre d’interpolation $p(t)$ .

Comment peut-on éliminer l’effet de

p(t)

L’effet de $p(t)$ peut être éliminé en appliquant un égaliseur (equalizer). L’égaliseur est l’équivalent d’un filtre passe bas ayant une fonction de transfert inverse (qui annule $p(t)$ ).
Soit ( E(f) ) la réponse en fréquence de l’égaliseur. Notre objectif de conception est d’obtenir

E(f) P(f) = \begin{cases} 0, & |f| \geq f_E - B \\ T_E e^{-j 2\pi f t_0}, & |f| < B \end{cases}

(11)

où $\textcolor{red}{t_0}$ est un délai qui assure la causalité du filtre conçu. Notez que nous nous concentrons uniquement sur la largeur de bande du message.

$Schéma du processus d’égalisation appliqué au signal reconstruit. Le signal \tilde{m}(t) , obtenu après interpolation, est traité par un égaliseur ayant une réponse impulsionnelle e(t) et une réponse en fréquence E(f) . L’objectif de ce filtrage est de compenser les distorsions introduites par le processus de transmission et de reconstruction, produisant ainsi un signal égalisé \bar{ \bar{m}}(t) , plus fidèle au signal d’origine.$

Figure 9:Schéma du processus d’égalisation appliqué au signal reconstruit. Le signal $\tilde{m}(t)$ , obtenu après interpolation, est traité par un égaliseur ayant une réponse impulsionnelle $e(t)$ et une réponse en fréquence $E(f)$ . L’objectif de ce filtrage est de compenser les distorsions introduites par le processus de transmission et de reconstruction, produisant ainsi un signal égalisé $\bar{ \bar{m}}(t)$ , plus fidèle au signal d’origine.

Quantification (Quantization)¶

Définition: Quantification: La quantification est la lecture d’un signal analogique avec une précision finie. Une conséquence importante de ce processus est l’ajout du bruit de quantification. La quantification est utilisée après l’échantillonnage dans le processus de numérisation d’un signal. Nous représenterons le signal après la quantification comme $\hat{m}(t)$

La quantification est un système qui transforme un signal d’entrée analogique à temps continu en un signal de sortie numérique à temps continu, en l’arrondissant à l’un des niveaux prédéfinis. Elle peut être représentée par une fonction de quantification

y = Q(x)

(12)

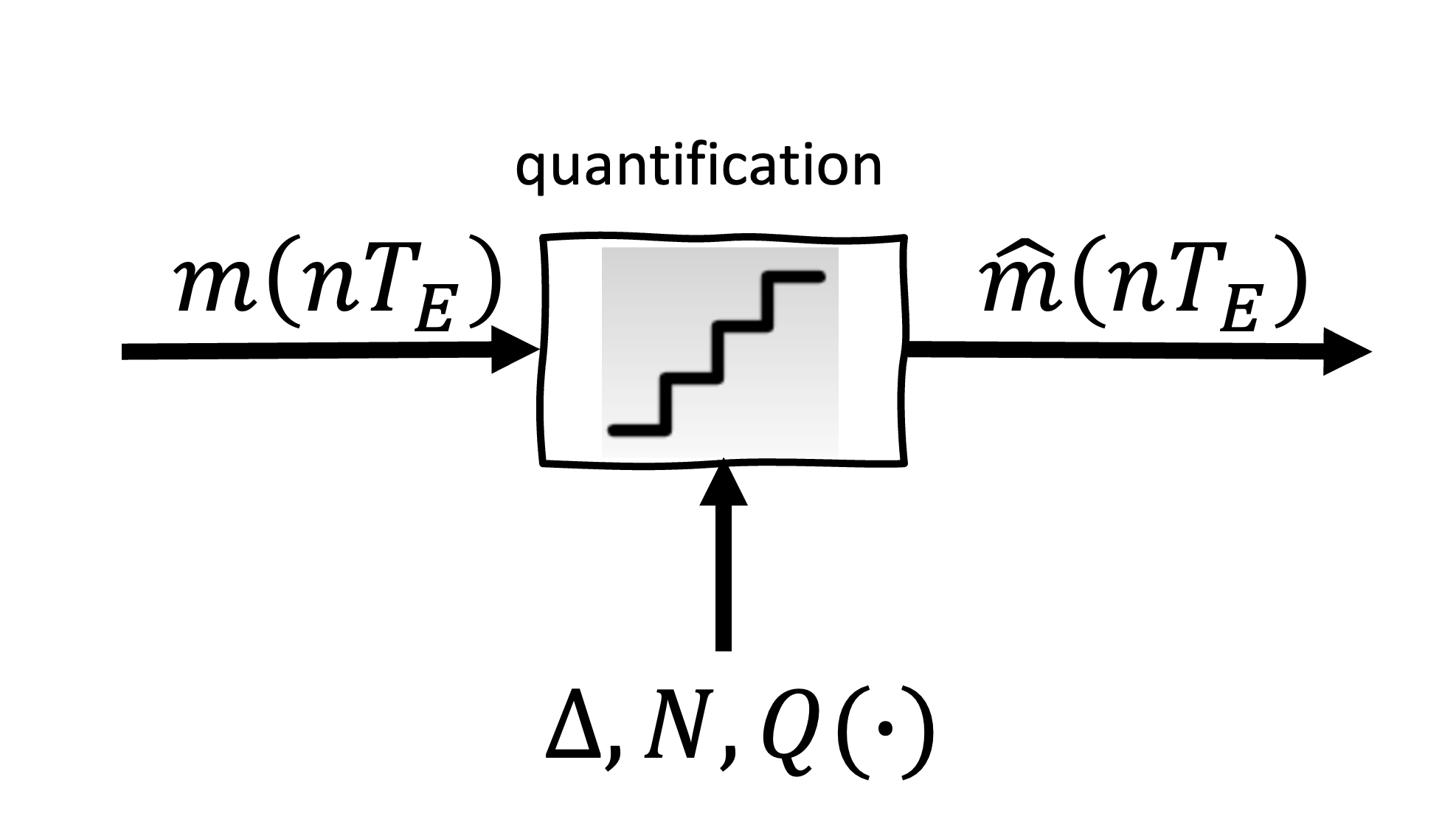
Schéma du processus de quantification. Le signal d’entrée m(nT_E) est mappé à un ensemble discret de valeurs de sortie \hat{m}(nT_E) . L’opération de quantification est définie par les paramètres \Delta (pas de quantification), N (nombre de bits pour representer 2^N niveaux de quantification) et Q(\cdot) (fonction de quantification). La fonction en escalier à l’intérieur du bloc représente les niveaux de quantification appliqués au signal d’entrée. — Figure 10:Schéma du processus de quantification. Le signal d’entrée $m(nT_E)$ est mappé à un ensemble discret de valeurs de sortie $\hat{m}(nT_E)$ . L’opération de quantification est définie par les paramètres $\Delta$ (pas de quantification), $N$ (nombre de bits pour representer $2^N$ niveaux de quantification) et $Q(\cdot)$ (fonction de quantification). La fonction en escalier à l’intérieur du bloc représente les niveaux de quantification appliqués au signal d’entrée.

Exemple illustratif :

Nombre de niveaux de quantification : ( 2^3 = 8 )
Marge de fonctionnement : de -4V à +4V
Pas de quantification Δ :
$\Delta = \frac{\text{plage de quantification}}{\text{nombre de niveaux}} = \frac{4 - (-4)}{8} = \frac{8}{8} = 1V$
(13)
Ainsi, chaque niveau est espacé de 1V.

Le signal est quantifié aux valeurs suivantes :

Entrée ([-4V, -3.5V]) → Quantifié à -3.5V
Entrée ([-3.5V, -2.5V]) → Quantifié à -2.5V
Entrée ([-2.5V, -1.5V]) → Quantifié à -1.5V
Entrée ([-1.5V, -0.5V]) → Quantifié à -0.5V
Entrée ([-0.5V, +0.5V]) → Quantifié à +0.5V
Entrée ([+0.5V, +1.5V]) → Quantifié à +1.5V
Entrée ([+1.5V, +2.5V]) → Quantifié à +2.5V
Entrée ([+2.5V, +3.5V]) → Quantifié à +3.5V

Toute valeur comprise dans un intervalle est arrondie au niveau de quantification le plus proche. Ce processus entraîne une erreur de quantification, qui dépend directement du pas de quantification Δ.

$Illustration du processus de quantification utilisant 3 bits, générant 2^3 = 8 niveaux de quantification dans une plage de -4V à +4V. L’intervalle de quantification est \Delta = 1V. Chaque valeur d’entrée m(nT_s) est arrondie au niveau de quantification le plus proche, produisant le signal quantifié \widetilde{m}(nT_s) . Cette quantification entraîne une erreur de quantification, qui dépend du pas de quantification \Delta = 1V .$

Figure 11:Illustration du processus de quantification utilisant 3 bits, générant $2^3 = 8$ niveaux de quantification dans une plage de -4V à +4V. L’intervalle de quantification est $\Delta = 1V$ . Chaque valeur d’entrée $m(nT_s)$ est arrondie au niveau de quantification le plus proche, produisant le signal quantifié $\widetilde{m}(nT_s)$ . Cette quantification entraîne une erreur de quantification, qui dépend du pas de quantification $\Delta = 1V$ .

Bruit de Quantification¶

Soit nombre total de niveaux disponibles représenté par $L$ par une fonction $y=Q(x)$ . On a besoin de $N$ bits pour chaque échantillon où

L = 2^N

(14)

Le bruit de quantification est l’erreur introduite après la quantification. Cette erreur est due à l’arrondi des valeurs du signal à l’un des niveaux de quantification disponibles.

L’échantillon quantifié est donné par :

\hat{m}(nT_E) = m(nT_E) + q(nT_E)

(15)

où $m(nT_E)$ est le signal de message (signal d’origine) et $q(nT_E)$ est le bruit de quantification ajouté.

La PDF du bruit $q(nT_E)$ est uniforme, et

-\frac{\Delta}{2} \leq q(nT_s) < \frac{\Delta}{2}

(16)

avec

\Delta = \frac{2m_p}{L}

(17)

où en général $-m_p \leq m(t) \leq m_p$ . Donc, on peut écrire la PDF du bruit de quantification comme :

p_Q(q) = \frac{1}{Delta}, \hspace{1cm} q\in \left[-\frac{\Delta}{2}, +\frac{\Delta}{2}\right]

(18)

Le bruit de quantification est centré en moyenne et sa valeur moyenne est

m_Q = E[q(nT_E)] = \int_{-\frac{\Delta}{2}}^{+\frac{\Delta}{2}}q p_Q(q)dq = 0,

(19)

et sa puissance est

E[q(nT_E)^2] = \int_{-\frac{\Delta}{2}}^{+\frac{\Delta}{2}}q^2 p_Q(q)dq = \frac{m_p^2}{3L^2}

(20)

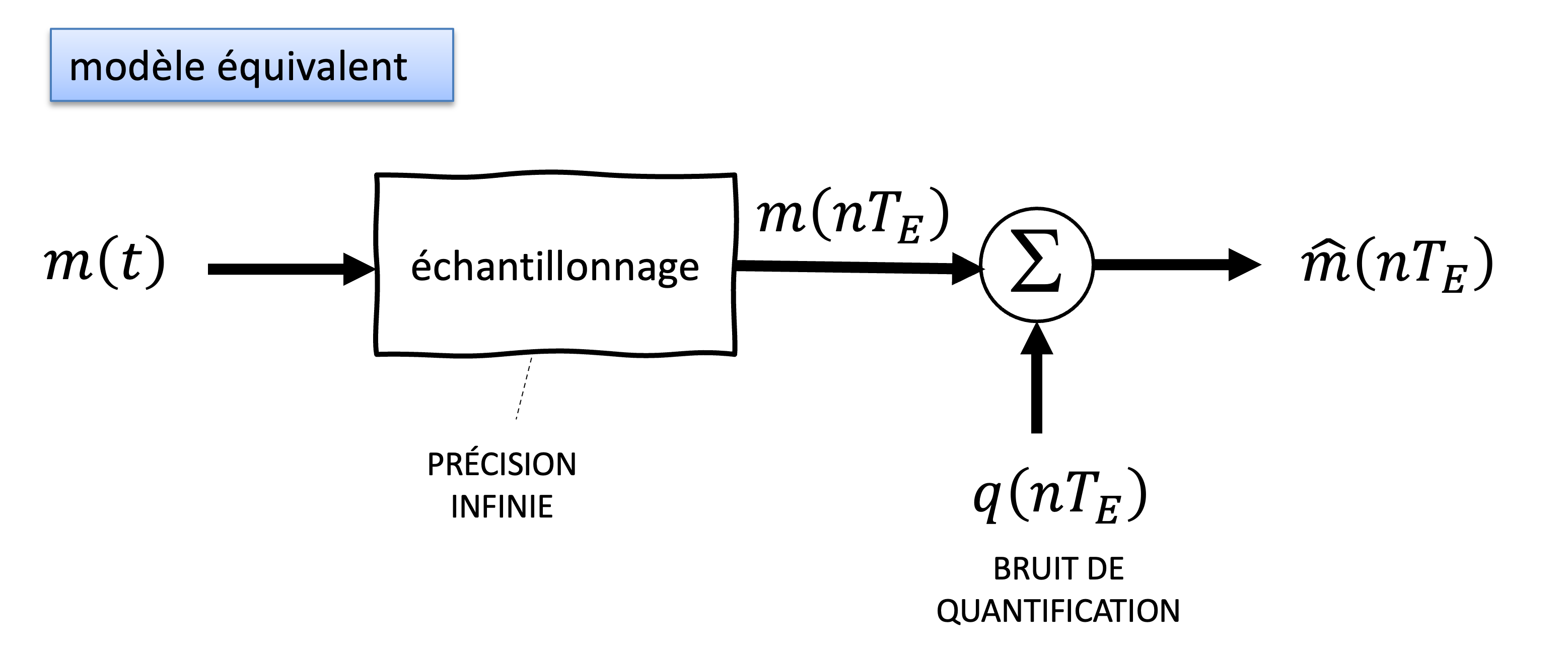
L’erreur est ajoutée au signal discrétisé, ce qui donne le signal quantifié \hat{m}(nT_E), utilisé pour la transmission ou le traitement numérique. La quantification introduit une distorsion, dont l’impact dépend du pas de quantification \Delta et du nombre de bits utilisés N. — Figure 12:L’erreur est ajoutée au signal discrétisé, ce qui donne le signal quantifié $\hat{m}(nT_E)$ , utilisé pour la transmission ou le traitement numérique. La quantification introduit une **distorsion**, dont l’impact dépend du pas de quantification $\Delta$ et du nombre de bits utilisés $N$ .

Le rapport signal sur bruit de quantification (signal-to-quantization-noise ratio; SQNR) est une mesure de la qualité du signal après quantification. Il est défini par :

SQNR = \frac{ \textrm{Puissance de } m(T_E)}{\textrm{Puissance de } q(nT_E)} = \frac{E[m^2(t)]}{E[q(nT_E)^2]} =3L^2 \frac{E[m^2(t)]}{m_p^2}

(21)

Le bruit de quantification est un facteur critique dans la conversion analogique-numérique, et il doit être minimisé pour assurer une haute fidélité du signal converti. Notez qu’un nombre de niveaux de quantification $L$ plus élevé réduit le bruit de quantification, mais mous avons besoin de plus de bits pour représenter les échantillons ( $N \times \textrm{le nombre total d'échantillons}$ ).

Types de fonctions de quantification¶

Il existe deux types de fonctions de quantification.

Quantification Uniforme : Lorsque les niveaux de quantification sont équidistants, on parle de quantification uniforme. L’intervalle entre chaque niveau est appelé pas de quantification (quantization step) $\Delta$ .
Quantification Non Uniforme : Utilisée lorsque certaines plages de valeurs doivent être plus précises (ex : compandage en télécommunications).

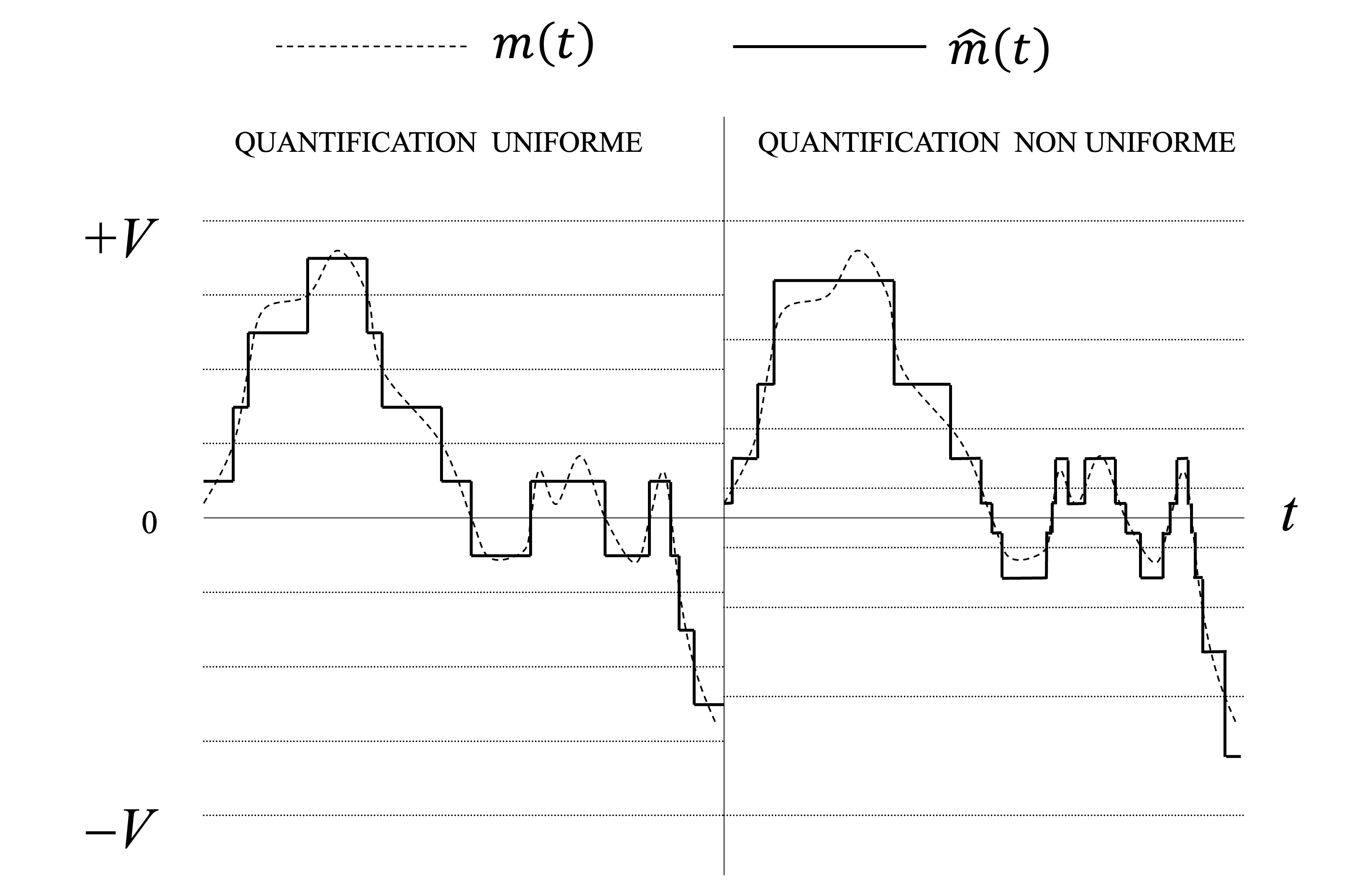
Figure 13:Exemples pour deux types de fonctions de quantification. Dans la quantification uniforme (à gauche), les niveaux sont répartis de manière égale sur toute la plage de signal, tandis que dans la quantification non uniforme (à droite), les niveaux sont plus denses pour les faibles amplitudes, réduisant ainsi l’erreur de quantification pour les signaux de faible intensité. Cette approche est couramment utilisée pour améliorer le rapport signal/bruit dans les systèmes de communication.

Applications: Modulations analogiques d’impulsions¶

La modulation analogique d’impulsions est une technique utilisée pour transmettre un signal analogique en modulant une série d’impulsions discrètes. Cette technique est largement employée en télécommunications et en traitement du signal. On utilise un signal de message qui porte l’information, $m(t)$ et une série d’impulsions (pulses) est utilisée pour moduler le signal, $p(t)$ . Le train d’impulsions est représentée par

\sum_{n=-\infty}^{\infty} p(t - nT_E)

(22)

où $p(t)$ est la forme de l’impulsion utilisée.

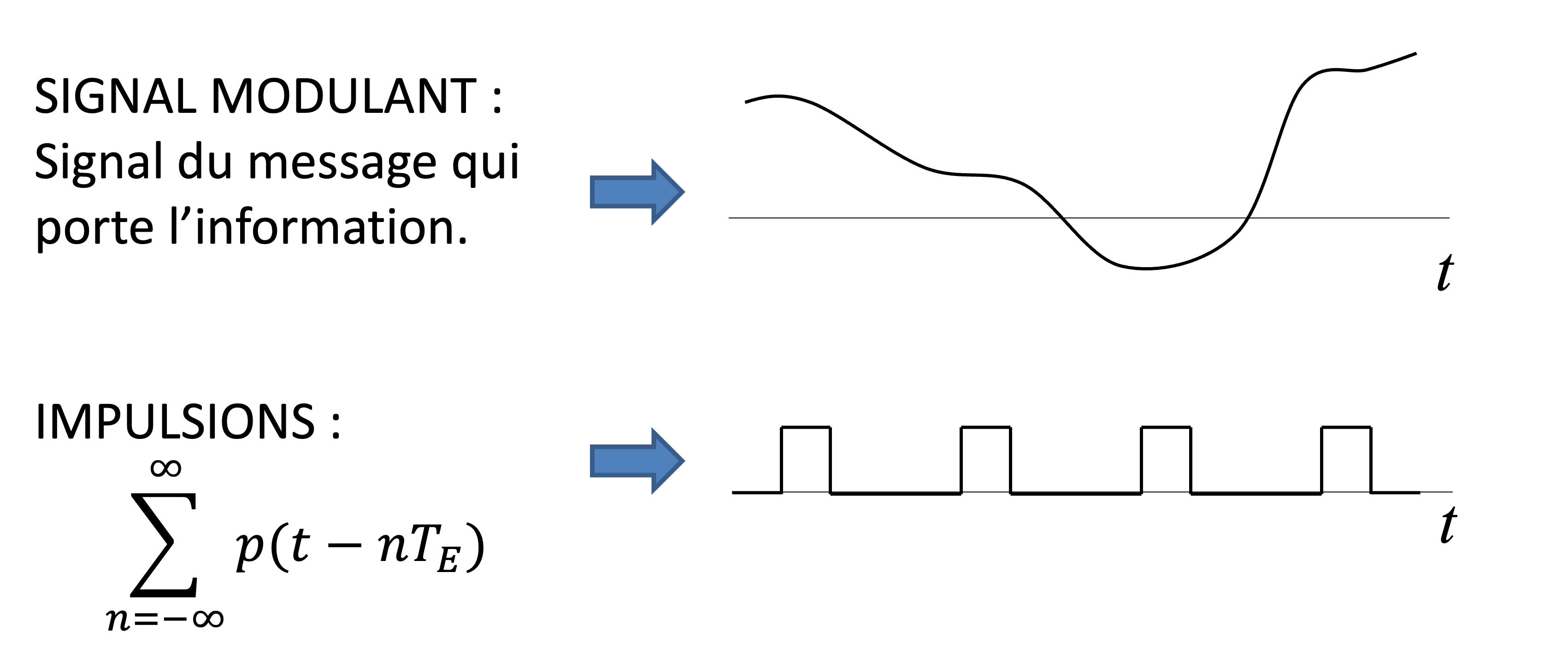
Illustration du processus d’échantillonnage à l’aide d’un train d’impulsions composé de p(t) avec une période de T_E seconds. — Figure 14:Illustration du processus d’échantillonnage à l’aide d’un train d’impulsions composé de $p(t)$ avec une période de $T_E$ seconds.

Ces impulsions serviront à coder le signal en utilisant différentes méthodes de modulation telles que :

PAM (Pulse Amplitude Modulation) : Modulation en amplitude des impulsions. L’amplitude des impulsions change.
PWM (Pulse Width Modulation) : Modulation de durée. La position des impulsions est la même, leur durée change.
PPM (Pulse Position Modulation) : Modulation en position des impulsions. La durée des impulsions est la même, leur position change.

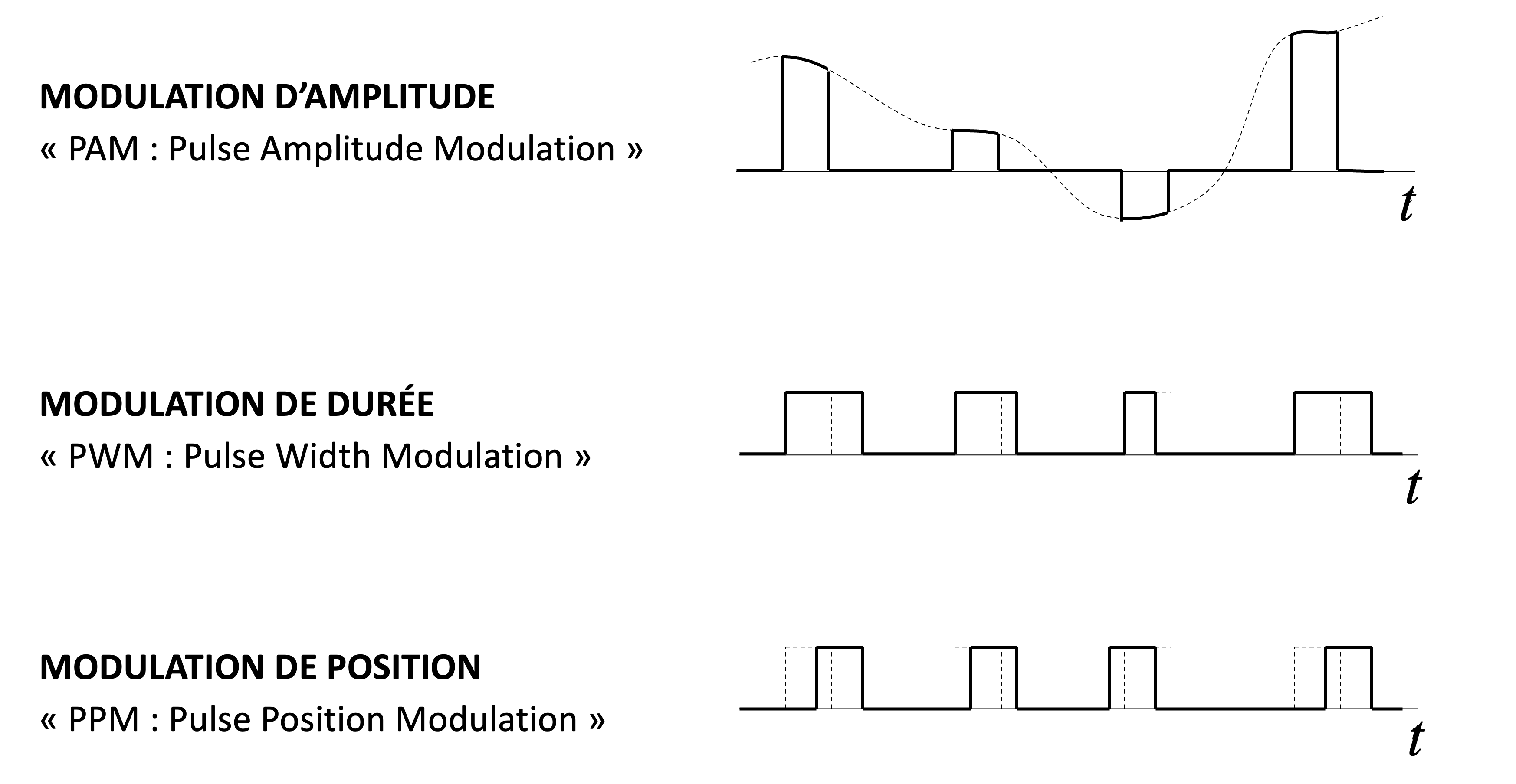
Figure 15:Une illustration de la PAM, PWM et PPM. (Voir: Exemples Intéractifs: Numérisation)

Modulation par impulsions codées (Pulse Code Modulation; PCM)¶

Modulation par impulsions codées (PCM) est un système pratique d’échantillonnage et de quantification.

La modulation par impulsions codées (PCM - Pulse Code Modulation) est une technique de numérisation utilisée pour convertir un signal analogique en un signal numérique. Elle se déroule en trois étapes principales :

Échantillonnage : Le signal analogique est prélevé à intervalles réguliers.
Quantification : Chaque échantillon est arrondi à l’un des $L$ niveaux disponibles.
Codage de ligne (line coding): Les niveaux quantifiés sont convertis en mots binaires.

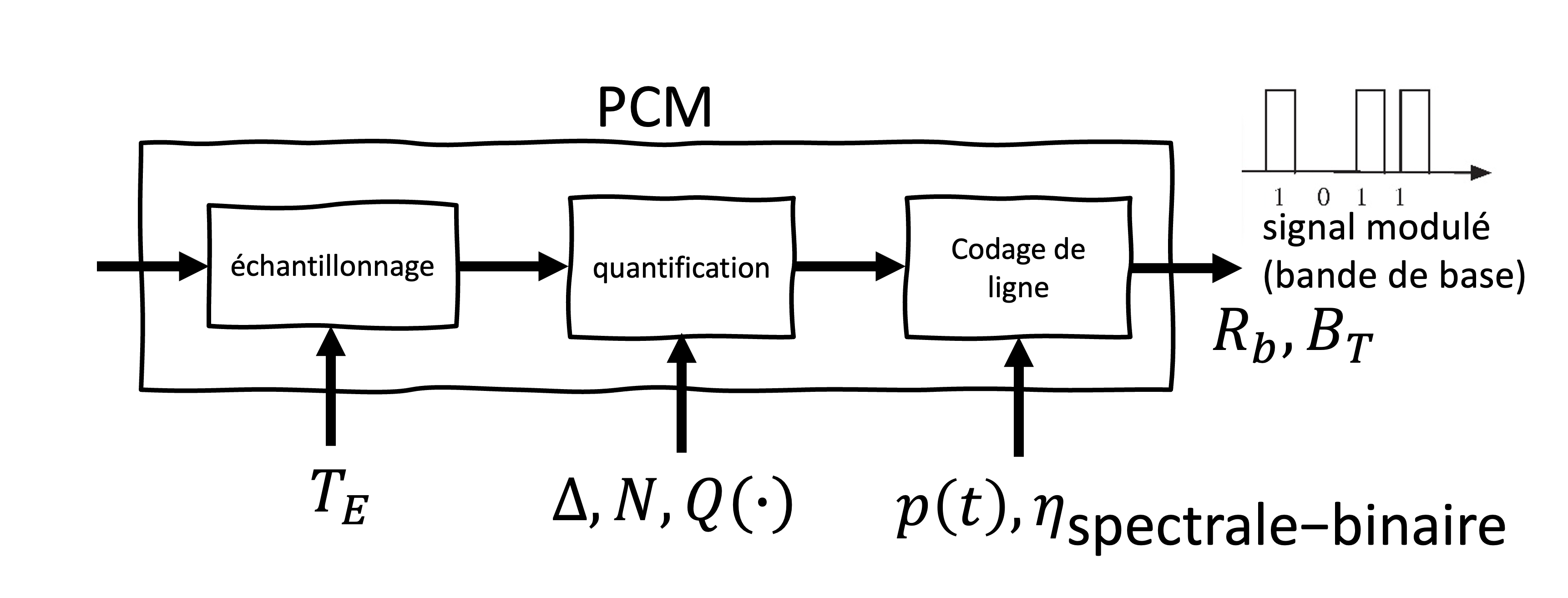
Schéma du processus de modulation par codage d’impulsions (PCM). Le signal analogique est d’abord échantillonné avec une période T_E, puis quantifié en utilisant \Delta, N, Q(\cdot) . Ensuite, un codage de ligne est appliqué à la séquence numérique via une fonction de codage p(t), influençant l’efficacité spectrale \eta_{\text{spectrale-binaire}} . En sortie, un signal modulé en bande de base (autour de 0 Hz) est obtenu, caractérisé par un débit binaire R_b et une largeur de bande B_T . — Figure 16:Schéma du processus de modulation par codage d’impulsions (PCM). Le signal analogique est d’abord échantillonné avec une période $T_E$ , puis quantifié en utilisant $\Delta, N, Q(\cdot)$ . Ensuite, un codage de ligne est appliqué à la séquence numérique via une fonction de codage $p(t)$ , influençant l’efficacité spectrale $\eta_{\text{spectrale-binaire}}$ . En sortie, un signal modulé en bande de base (autour de 0 Hz) est obtenu, caractérisé par un débit binaire $R_b$ et une largeur de bande $B_T$ .

La quantification est une étape essentielle du système PCM, où chaque échantillon $m(nT_E)$ du signal $m(t)$ est approximé par l’un des $L$ niveaux de quantification et

\Delta = \frac{2m_p}{L}

(23)

Exemple illustratif :

le nombre total de niveaux est :

L = 8

(24)

et le nombre de bits nécessaires pour coder chaque échantillon est :

N = \log_2(L) = \log_2(8) = 3 \text{ bits}.

(25)

$Schéma de la modulation par impulsions codées (PCM) avec quantification sur 3 bits par échantillon. Le signal d’origine m(t) (en rouge) est échantillonné à des intervalles T_E et quantifié en niveaux discrets avec un pas \Delta . Le signal varie entre m_p = 4V et -m_p = -4V, ce qui signifie que son amplitude totale est de 2m_p, 8V. Comme la quantification utilise 3 bits, cela implique qu’il y a 2^3 = 8 niveaux de quantification. Donc, chaque intervalle de quantification \Delta correspond à 8/8= 1 V. Chaque valeur quantifiée est ensuite encodée en binaire, illustrant le processus de conversion du signal analogique en numérique.$

Figure 17:Schéma de la modulation par impulsions codées (PCM) avec quantification sur 3 bits par échantillon. Le signal d’origine $m(t)$ (en rouge) est échantillonné à des intervalles $T_E$ et quantifié en niveaux discrets avec un pas $\Delta$ . Le signal varie entre $m_p = 4$ V et $-m_p = -4$ V, ce qui signifie que son amplitude totale est de $2m_p$ , 8V. Comme la quantification utilise 3 bits, cela implique qu’il y a $2^3 = 8$ niveaux de quantification. Donc, chaque intervalle de quantification $\Delta$ correspond à $8/8= 1$ V. Chaque valeur quantifiée est ensuite encodée en binaire, illustrant le processus de conversion du signal analogique en numérique.

À la sortie du système PCM, nous avons un signal binaire caractérisé par deux paramètres de conception :

$R_b$ : Débit binaire, en bits/sec.
$B_T$ : Largeur de bande requise, en Hz.

Les paramètres $R_b$ et $B_T$ sont influencés par la forme d’impulsion $p(t)$ utilisée pour coder les bits. Différents schémas de codage binaire, comme NRZ (Non-Return to Zero) ou Manchester (line coding), affectent l’efficacité spectrale du signal transmis.

Pour concevoir le système de communication, on doit definir l’efficacité spectrale binaire

\eta_{\text{spectrale-binaire}} = \frac{R_b}{B_T} \quad \text{bits/sec/Hz}

(26)

Elle exprime le nombre de bits transmis par seconde et par Hz de bande passante.

D’après le théorème de Nyquist, l’efficacité spectrale maximale pour un signal binaire sans interférence intersymbole (inter symbol interference; ISI) est :

\eta_{\text{spectrale-binaire}} \leq 2 \text{ bits/sec/Hz}

(27)

Cela signifie que, dans un canal idéal, un débit binaire maximum de $2B_T$ bits/sec peut être atteint en utilisant des impulsions optimales.

Multiplexage temporel (Time Division Multiplexing)¶

Définition: Multiplexage temporel: Le multiplexage temporel (Time Division Multiplexing; TDM) est une technique permettant de combiner plusieurs signaux utilisateurs en un seul flux (flow) de transmission en allouant des intervalles de temps distincts à chaque signal.

Exemple pratique : Système T1 de BELL

Le système T1, utilisé en télécommunications, applique le multiplexage temporel pour transmettre plusieurs canaux vocaux sur une seule ligne. Les principales étapes sont :

Échantillonnage des canaux (pour chaqe utilisateur)
- 24 canaux vocaux sont échantillonnés en séquence à un taux de 8 kHz.
Multiplexage PAM
- Après échantillonnage, la sortie représente un signal PAM où chaque échantillon est multiplexé par répartition temporelle.
Quantification et codage (line coding)
- Chaque échantillon est quantifié et converti en un mot de 8 bits par un convertisseur analogique-numérique (ADC). La sortie est une séquence binaire.
Transmission du signal numérique
- Le signal numérisé et multiplexé est ensuite transmis sur une ligne dédiée.

Le calcul pour le débit binaire total du système T1 :

Nombre de canaux : $24$
Fréquence d’échantillonnage par canal : $f_E = 8$ kHz
Nombre de bits par échantillon : $N = 8$

Le débit binaire total $R_b$ est donné par :

R_b = \text{Nombre de canaux} \times \text{Fréquence d’échantillonnage} \times \text{Bits par échantillon}

(28)

R_b = 24 \times 8 \times 10^3 \times 8 = 1.536 \text{ Mbps}

(29)

Format de la Trame¶

Définition: Trame: Une trame (frame) est un segment contenant un mot de code (échantillon) pour chacun des canaux dans un système.

Exemple pratique : Structure de la Trame dans un Système T1

Dans un système T1, l’organisation des données suit ces étapes :

Chaque canal est échantillonné et converti en un mot de code de 8 bits.
Une trame contient un mot de code pour chaque canal.
La structure de la trame est donc :
$24 \times 8 = 192 \text{ bits}$
(30)
Ainsi, une trame transporte 192 bits d’information.

Le taux de trame est de :

8000 \text{ trames/sec}

(31)

Cela correspond à la fréquence d’échantillonnage des signaux audio téléphoniques de 8 kHz.

Chaque trame a une durée de :

T_{\text{trame}} = \frac{1}{8000} = 125 \ \mu s

(32)

Chaque canal vocal est échantillonné à 8 kHz, donc un nouvel échantillon est pris toutes les 125 µs. Le système doit donc transmettre une trame complète chaque 125 µspour garantir la synchronisation et la qualité du signal.

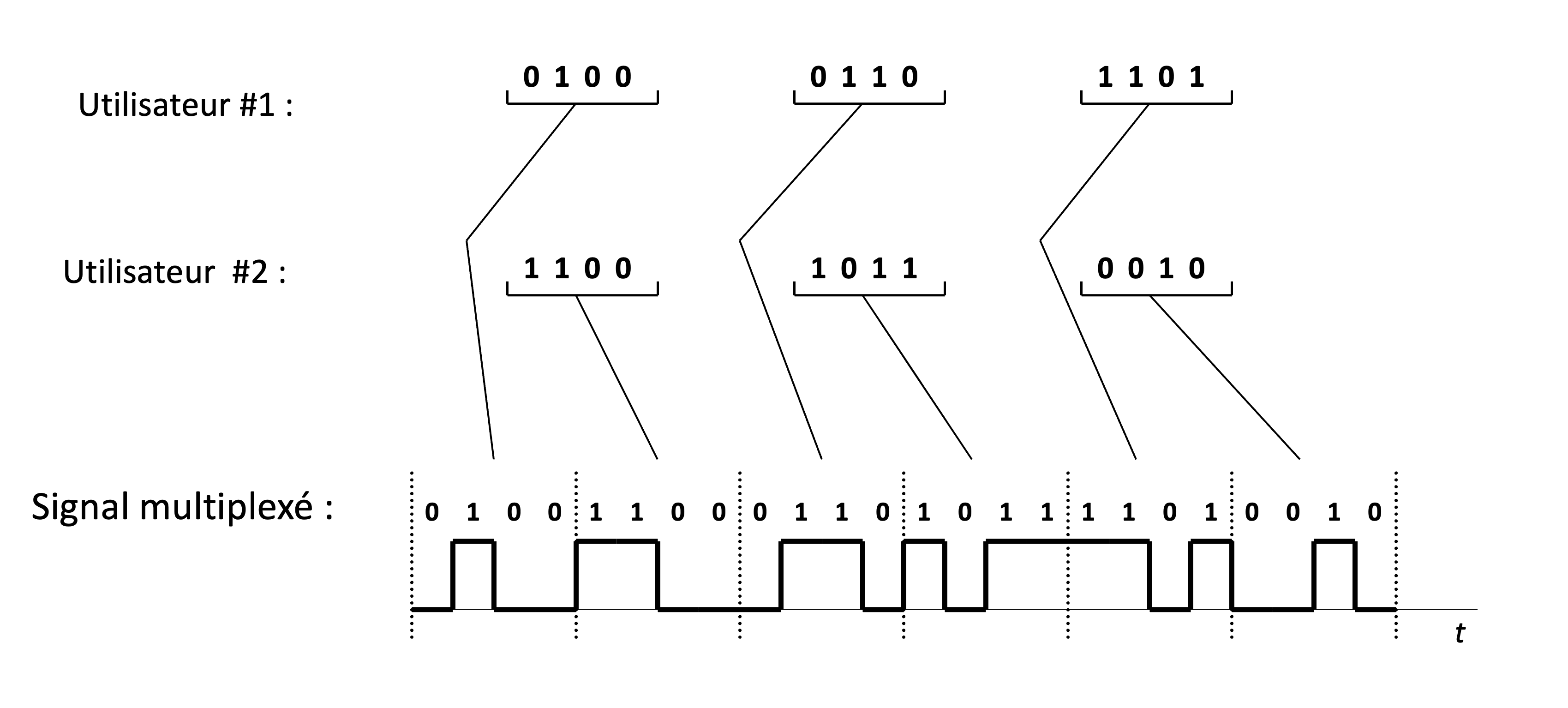
Un exemple de multiplexage temporel (TDM) avec deux utilisateurs. Si chaque utilisateur transmet à un débit de R_b bits/seconde, alors la trame TDM doit être transmise à un débit de 2R_b bits/seconde. Cela est nécessaire pour préserver l’intégrité des données de chaque utilisateur et garantir que toutes les informations sont transmises sans perte. — Figure 18:Un exemple de multiplexage temporel (TDM) avec deux utilisateurs. Si chaque utilisateur transmet à un débit de $R_b$ bits/seconde, alors la trame TDM doit être transmise à un débit de $2R_b$ bits/seconde. Cela est nécessaire pour préserver l’intégrité des données de chaque utilisateur et garantir que toutes les informations sont transmises sans perte.

Dans un système de TDM (comme le T1), les données sont transmises en trames successives. Pour que le récepteur puisse identifier correctement les données et éviter tout décalage, il doit connaître la position de chaque trame. Pour cette raison, un bit de cadrage (framing bit) est ajouté au début de chaque trame. Ce bit permettre au récepteur de détecter le début de chaque trame. Donc il sert de repère temporel et assure la synchronisation entre l’émetteur et le récepteur.

Resumé¶

Cette section traite de O3 Numérisation des signaux : Comprendre l’échantillonnage, la quantification, et les conversions analogique-numérique, qui concerne la numérisation des signaux, englobant l’échantillonnage, la quantification et les conversions analogique-numérique. La numérisation repose sur plusieurs paramètres influençant la qualité et l’efficacité de la transmission. L’échantillonnage est caractérisé par sa fréquence $f_E$ , qui doit être au moins égale à $2B$ pour éviter l’aliasing, conformément au théorème de Nyquist, ainsi que par la période d’échantillonnage $T_E = \frac{1}{f_E}$ . La quantification implique l’approximation de chaque échantillon à un niveau discret parmi $L$ niveaux possibles, où le nombre de bits par échantillon est déterminé par $n = \log_2 L$ , générant un bruit de quantification . La PCM convertit ces échantillons en séquences binaires, définissant un débit binaire $R_b = 2nB$ , qui détermine la bande passante requise $B_T = \frac{R_b}{\eta_{\text{spectrale}}}$ , avec une limite maximale de 2 bits/sec/Hz selon Nyquist. Le multiplexage temporel (TDM) regroupe les canaux des utilisateurs dans une trame unique, comprenant des bits de cadrage essentiel pour assurer la synchronisation entre l’émetteur et le récepteur. Une conception optimisée de ces paramètres permet d’assurer une transmission efficace et adaptée aux contraintes de bande passante d’un canal.

Introduction

Section 2 - Notions fondamentales

Introduction

Exemples Intéractifs: Numérisation